题目内容
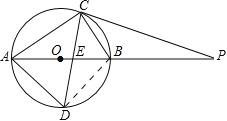
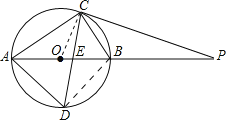
【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.

(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
【答案】(1)AC=8,AD=5![]() cm;(2)直线PC与⊙O相切,理由见解析.
cm;(2)直线PC与⊙O相切,理由见解析.
【解析】试题分析:(1)、连接BD,根据AB为直径,则∠ACB=∠ADB=90°,根据Rt△ABC的勾股定理求出AC的长度,根据CD平分∠ACB得出Rt△ABD是等腰直角三角形,从而得出AD的长度;(2)、连接OC,根据OA=OC得出∠CAO=∠OCA,根据PC=PE得出∠PCE=∠PEC,然后结合CD平分∠ACB得出∠ACE=∠ECB,从而得出∠PCB=∠ACO,根据∠ACB=90°得出∠OCP=90°,从而说明切线.
试题解析:(1)、①如图,连接BD, ∵AB是直径, ∴∠ACB=∠ADB=90°,
在RT△ABC中,AC=![]() =
=![]() =8cm,
=8cm,
②∵CD平分∠ACB, ∴AD=BD,∴Rt△ABD是直角等腰三角形, ∴AD=![]() AB=
AB=![]() ×10=5
×10=5![]() cm;
cm;
(2)、直线PC与⊙O相切,
理由:连接OC, ∵OC=OA,∴∠CAO=∠OCA, ∵PC=PE, ∴∠PCE=∠PEC,
∵∠PEC=∠CAE+∠ACE, ∵CD平分∠ACB, ∴∠ACE=∠ECB,∴∠PCB=∠ACO,∵∠ACB=90°,
∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°, OC⊥PC,
∴直线PC与⊙O相切.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

