题目内容
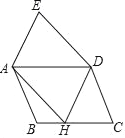
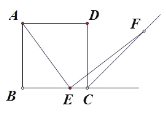
【题目】如图,四边形 ABCD 是正方形,点 E是 BC边上任意一点, AEF 90°,且EF 交正方形外角的平分线 CF 于点 F.求证:AE=EF.
【答案】见解析
【解析】
截取BE=BM,连接EM,求出AM=EC,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可.
证明:在AB上截取BM=BE,连接ME,
∵∠B=90°,
∴∠BME=∠BEM=45°,
∴∠AME=135°
∵CF是正方形ABCD的外角的角平分线,
∴∠ECF=90°+∠DCF=90°+![]() =135°=∠ECF,
=135°=∠ECF,
∵AEF 90°
∴∠AEB+![]() =90°
=90°
又∠AEB+![]() =90°,
=90°,
∴![]()
∵AB=BC,BM=BE,
∴AM=EC,
在△AME和△ECF中
 ,
,
∴△AME≌△ECF(ASA),
∴AE=EF.


练习册系列答案
相关题目