题目内容
在平面直角坐标系xOy中,抛物线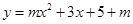 与x轴交于A、B两点(点A
与x轴交于A、B两点(点A
在点B的左侧),与y轴交于点C(0 , 4),D为OC的中点.
小题1:(1)求m的值;
小题2:(2)抛物线的对称轴与x轴交于点E,在直线AD上是否存在点F,使得以点A、B、F为顶点的三角形与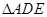 相似?若存在,请求出点F的坐标,若不存在,请说明理由;
相似?若存在,请求出点F的坐标,若不存在,请说明理由;
小题3:(3)在抛物线的对称轴上是否存在点G,使△GBC中BC边上的高为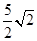 ?若存在,求出点G的坐标;若不存在,请说明理由.
?若存在,求出点G的坐标;若不存在,请说明理由.
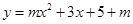 与x轴交于A、B两点(点A
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0 , 4),D为OC的中点.
小题1:(1)求m的值;
小题2:(2)抛物线的对称轴与x轴交于点E,在直线AD上是否存在点F,使得以点A、B、F为顶点的三角形与
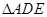 相似?若存在,请求出点F的坐标,若不存在,请说明理由;
相似?若存在,请求出点F的坐标,若不存在,请说明理由; 小题3:(3)在抛物线的对称轴上是否存在点G,使△GBC中BC边上的高为
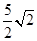 ?若存在,求出点G的坐标;若不存在,请说明理由.
?若存在,求出点G的坐标;若不存在,请说明理由.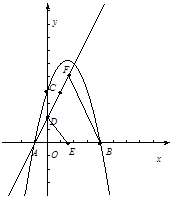
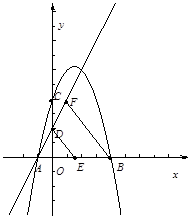
小题1:解:(1)抛物线
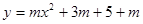 与y轴交于点C(0 , 4),
与y轴交于点C(0 , 4), ∴

∴
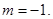
小题2:(2)抛物线的解析式为
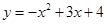 .
.可求抛物线与x轴的交点A(-1,0),B(4,0).
可求点E的坐标
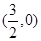 .
.由图知,点F在x轴下方的直线AD上时,
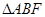 是钝角三角形,不可能与
是钝角三角形,不可能与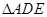 相似,所以点F一定在x轴上方.
相似,所以点F一定在x轴上方.此时
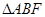 与
与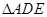 有一个公共角,两
有一个公共角,两 个三角形相似存在两种情况:
个三角形相似存在两种情况:① 当
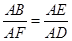 时,由于E为AB的中点,此时D为AF的中点,
时,由于E为AB的中点,此时D为AF的中点,可求 F点坐标为(1,4). ………3分
② 当
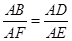 时,
时,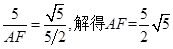 .
.过F点作FH⊥x轴,垂足为H.
可求 F的坐标为
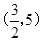 . ……………4分
. ……………4分(3)
(4)
小题3:(3) 在抛物线的对称轴上存在符合题意的点G .
由题意,可知△OBC为等腰直角三角形,直线BC为
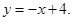
可求与直线BC平行且的距离为
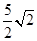 的直线为 y=-x+9或y=-x-1.
的直线为 y=-x+9或y=-x-1.…………………6分
∴ 点G在直线y=-x+9或y=-x-1上.
∵ 抛物线的对称轴是直线
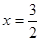 ,
,∴
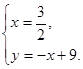 解得
解得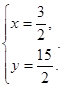
或
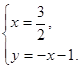 解得
解得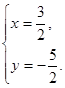
∴ 点
 G的坐标为
G的坐标为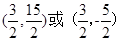 .
. 略

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
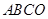 的边
的边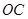 落在
落在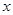 轴的正半轴上,且
轴的正半轴上,且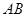 ∥
∥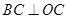 ,
,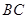 =6,
=6,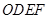 的两边分别落在坐标轴上,且它的面积等于直角梯形
的两边分别落在坐标轴上,且它的面积等于直角梯形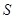 。
。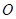 移动到点
移动到点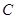 时,求
时,求

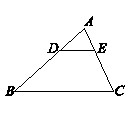
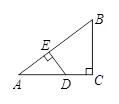
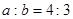 ,则下列各式中正确的式子是( ).
,则下列各式中正确的式子是( ).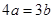 B.
B.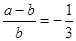 C.
C.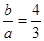 D.
D.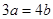
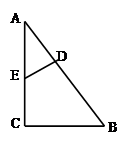
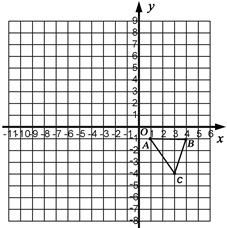
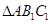 ,并写出点
,并写出点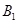 的坐标:
的坐标: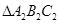 ,使得它与△ABC的位似比等于2:1 .
,使得它与△ABC的位似比等于2:1 .