题目内容
如图,在平面直角坐标系xOy中,二次函数 (a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
(a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
(1)求a和b的值;
(2)求t的取值范围;
(3)若∠PCQ=90°,求t的值.
(1)
(2)t>﹣4
(3)t=﹣2
解析分析:(1)将点A、点B的坐标代入二次函数解析式可求出a、b的值。
(2)根据二次函数及y=t,可得出方程,有两个交点,可得△>0,求解t的范围即可。
(3)证明△PDC∽△CDQ,利用相似三角形的对应边成比例,可求出t的值。
解:(1)将点A、点B的坐标代入可得: ,解得:
,解得: 。
。
(2)抛物线的解析式为 ,直线y=t,
,直线y=t,
联立两解析式可得:x2+2x﹣3=t,即x2+2x﹣(3+t)=0,
∵动直线y=t(t为常数)与抛物线交于不同的两点,
∴△=4+4(3+t)>0,解得:t>﹣4。
(3)∵y=x2+2x﹣3=(x+1)2﹣4,
∴抛物线的对称轴为直线x=1。
当x=0时,y=﹣3,∴C(0,﹣3)。
设点Q的坐标为(m,t),则P(﹣2﹣m,t)。
如图,设PQ与y轴交于点D,
则CD=t+3,DQ=m,DP=m+2。
∵∠PCQ=∠PCD+∠QCD=90°,∠DPC+∠PCD=90°,∴∠QCD=∠DPC。
又∠PDC=∠QDC=90°,∴△QCD∽△CDP。∴ ,即
,即 。
。
整理得:t2+6t+9=m2+2m。
∵Q(m,t)在抛物线上,∴t=m2+2m﹣3,即m2+2m=t+3。
∴t2+6t+9=t+3,化简得:t2+5t+6=0,解得t=﹣2或t=﹣3。
当t=﹣3时,动直线y=t经过点C,故不合题意,舍去。
∴t=﹣2。

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
已知反比例函数y= ,下列结论中不正确的是( )
,下列结论中不正确的是( )
| A.图象必经过点(1,﹣5) | B.y随x的增大而增大 |
| C.图象在第二、四象限内 | D.若x>1,则﹣5<y<0 |
 ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).

 .
.
 经过点A、B、C.
经过点A、B、C.
 与直线
与直线 交于C,D两点,其中点C在y轴上,点D的坐标为
交于C,D两点,其中点C在y轴上,点D的坐标为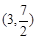 。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
 (k≠0)上,将正方形沿x轴负方向平移 m个单位长度后,点C恰好落在双曲线上,则m的值是 ( )
(k≠0)上,将正方形沿x轴负方向平移 m个单位长度后,点C恰好落在双曲线上,则m的值是 ( )