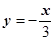题目内容
如图,在平面直角坐标系中,A(1,0),B(0,3),以AB为边在第一象限作正方形ABCD,点D在双曲线y= (k≠0)上,将正方形沿x轴负方向平移 m个单位长度后,点C恰好落在双曲线上,则m的值是 ( )
(k≠0)上,将正方形沿x轴负方向平移 m个单位长度后,点C恰好落在双曲线上,则m的值是 ( )
| A.2 | B.3 | C. | D.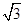 |
A.
解析试题分析:作CE⊥y轴于点E,交双曲线于点G.作DF⊥x轴于点F.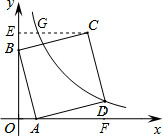
∵A(1,0),B(0,3),
∴OB=3,OA=1.
∵∠BAD=90°,
∴∠BAO+∠DAF=90°,
又∵直角△ABO中,∠BAO+∠OBA=90°,
∴∠DAF=∠OBA,
在△OAB和△FDA中,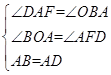 ,
,
∴△OAB≌△FDA(AAS),
同理,△OAB≌△FDA≌△BEC,
∴AF=OB=EC=3,DF=OA=BE=1,
故D的坐标是(4,1),C的坐标是(3,4).代入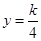 得:k=4,
得:k=4,
则函数的解析式是: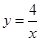 .
.
OE=4,
则C的纵坐标是4,把y=4代入y=得:x=1.即G的坐标是(1,4),
∴CG=2.
故选A.
考点:1.正方形的性质;2.反比例函数图象上点的坐标特征;3.平移的性质.

练习册系列答案
相关题目
在下列叙述中:
①一组对边相等的四边形是平行四边形;
②函数y= 中,y随x的增大而减小;
中,y随x的增大而减小;
③有一组邻边相等的平行四边形是菱形;
④有不可能事件A发生的概率为0.0001.
正确的叙述有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
点A在双曲线 上,AB⊥x轴于B,且△AOB的面积为3,则k=( )
上,AB⊥x轴于B,且△AOB的面积为3,则k=( )
| A.3 | B.6 | C.±3 | D.±6 |
已知反比例函数y=﹣ 的图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,则下列判断正确的是()
的图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,则下列判断正确的是()
| A.y1<y2<0 | B.0<y2<y1 | C.y1<0<y2 | D.y2<0<y1 |
已知点P(-1,3)在反比例函数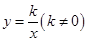 的图象上,则k的值是 ( )
的图象上,则k的值是 ( )
A.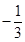 | B.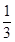 | C.3 | D.-3 |
点(-1,y1),(2,y2),(3,y3)均在函数y=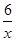 的图象上,则y1,y2,y3的大小关系是( )
的图象上,则y1,y2,y3的大小关系是( )
| A.y3<y2<y1 | B.y2<y3<y1 |
| C.y1<y2<y3 | D.y1<y3<y2 |
 (a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
(a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
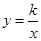 (k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
(k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )