题目内容
已知抛物线y=a(x﹣3)2+2经过点(1,﹣2).
(1)求a的值;
(2)若点A(m,y1)、B(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
(1)a=﹣1 (2)y1<y2
解析试题分析:(1)将点(1,﹣2)代入y=a(x﹣3)2+2,运用待定系数法即可求出a的值。;
(2)先求得抛物线的对称轴为x=3,再判断A(m,y1)、B(n,y2)(m<n<3)在对称轴左侧,从而判断出y1与y2的大小关系。
解:(1)∵抛物线y=a(x﹣3)2+2经过点(1,﹣2),
∴﹣2=a(1﹣3)2+2,解得a=﹣1。
(2)∵函数y=﹣(x﹣3)2+2的对称轴为x=3,
∴A(m,y1)、B(n,y2)(m<n<3)在对称轴左侧。
又∵抛物线开口向下,∴对称轴左侧y随x的增大而增大。
∵m<n<3,∴y1<y2

练习册系列答案
相关题目
“绿色出行,低碳健身”已成为广大市民的共识.某旅游景点新增了一个公共自行车停车场,6:00至18:00市民可在此借用自行车,也可将在各停车场借用的自行车还于此地.林华同学统计了周六该停车场各时段的借、还自行车数,以及停车场整点时刻的自行车总数(称为存量)情况,表格中x=1时的y值表示7:00时的存量,x=2时的y值表示8:00时的存量…依此类推.他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
| 时段 | x | 还车数(辆) | 借车数(辆) | 存量y(辆) |
| 6:00﹣7:00 | 1 | 45 | 5 | 100 |
| 7:00﹣8:00 | 2 | 43 | 11 | n |
| … | … | … | … | … |
(1)m= ,解释m的实际意义: ;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知9:00~10:00这个时段的还车数比借车数的3倍少4,求此时段的借车数.

函数的自变量x满足 时,函数值y满足
时,函数值y满足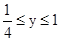 ,则这个函数可以是( )
,则这个函数可以是( )
A. | B. | C. | D. |
点A在双曲线 上,AB⊥x轴于B,且△AOB的面积为3,则k=( )
上,AB⊥x轴于B,且△AOB的面积为3,则k=( )
| A.3 | B.6 | C.±3 | D.±6 |


 与x轴交于A.B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(﹣1,0).
与x轴交于A.B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(﹣1,0).
 (a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
(a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
 与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).
与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).