题目内容
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).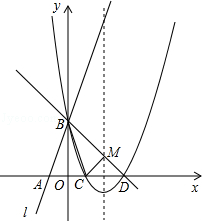
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
(1)直线BD的解析式为:y=﹣x+3。
抛物线的解析式为:y=(x﹣1)(x﹣3)=x2﹣4x+3。
(2)满足条件的点N坐标为:(0,0),(﹣3,0)或(0,﹣3)。
(3)存在,理由见解析。
解析分析:(1)由待定系数法求出直线BD和抛物线的解析式。
(2)首先确定△MCD为等腰直角三角形,因为△BND与△MCD相似,所以△BND也是等腰直角三角形.如答图1所示,符合条件的点N有3个。
(3)如答图2、答图3所示,解题关键是求出△PBD面积的表达式,然后根据S△PBD=6的已知条件,列出一元二次方程求解。
解:(1)∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,
∴A(﹣1,0),B(0,3)。
∵把△AOB沿y轴翻折,点A落到点C,∴C(1,0)。
设直线BD的解析式为:y=kx+b,
∵点B(0,3),D(3,0)在直线BD上,
∴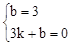 ,解得
,解得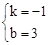 。
。
∴直线BD的解析式为:y=﹣x+3。
设抛物线的解析式为:y=a(x﹣1)(x﹣3),
∵点B(0,3)在抛物线上,∴3=a×(﹣1)×(﹣3),解得:a=1。
∴抛物线的解析式为:y=(x﹣1)(x﹣3)=x2﹣4x+3。
(2)∵抛物线的解析式为:y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,﹣1)。
直线BD:y=﹣x+3与抛物线的对称轴交于点M,令x=2,得y=1,∴M(2,1)。
设对称轴与x轴交点为点F,则CF=FD=MN=1,
∴△MCD为等腰直角三角形。
∵以点N、B、D为顶点的三角形与△MCD相似,∴△BND为等腰直角三角形。
如答图1所示: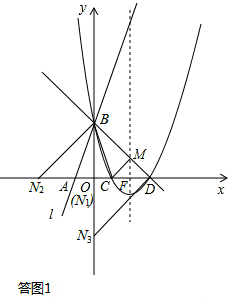
(I)若BD为斜边,则易知此时直角顶点为原点O,
∴N1(0,0)。
(II)若BD为直角边,B为直角顶点,则点N在x轴负半轴上,
∵OB=OD=ON2=3,∴N2(﹣3,0)。
(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,
∵OB=OD=ON3=3,∴N3(0,﹣3)。
∴满足条件的点N坐标为:(0,0),(﹣3,0)或(0,﹣3)。
(3)存在,
假设存在点P,使S△PBD=6,设点P坐标为(m,n),
(I)当点P位于直线BD上方时,如答图2所示,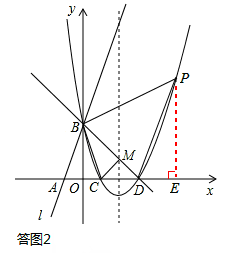
过点P作PE⊥x轴于点E,则PE=n,DE=m﹣3,
S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE
= (3+n)•m﹣
(3+n)•m﹣ ×3×3﹣
×3×3﹣ (m﹣3)•n=6,
(m﹣3)•n=6,
化简得:m+n="7" ①。
∵P(m,n)在抛物线上,
∴n=m2﹣4m+3,代入①式整理得:m2﹣3m﹣4=0,
解得:m1=4,m2=﹣1。
∴n1=3,n2=8。
∴P1(4,3),P2(﹣1,8)。
(II)当点P位于直线BD下方时,如答图3所示,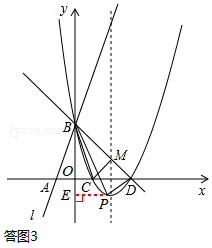
过点P作PE⊥y轴于点E,
则PE=m,OE=﹣n,BE=3﹣n,
S△PBD=S梯形PEOD+S△BOD﹣S△PBE= (3+m)•(﹣n)+
(3+m)•(﹣n)+ ×3×3﹣
×3×3﹣ (3﹣n)•m=6,
(3﹣n)•m=6,
化简得:m+n=﹣1 ②。
∵P(m,n)在抛物线上,∴n=m2﹣4m+3。
代入②式整理得:m2﹣3m+4=0,△=﹣7<0,此方程无解.
∴此时点P不存在。
综上所述,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(﹣1,8)。

 阅读快车系列答案
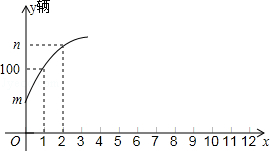
阅读快车系列答案“绿色出行,低碳健身”已成为广大市民的共识.某旅游景点新增了一个公共自行车停车场,6:00至18:00市民可在此借用自行车,也可将在各停车场借用的自行车还于此地.林华同学统计了周六该停车场各时段的借、还自行车数,以及停车场整点时刻的自行车总数(称为存量)情况,表格中x=1时的y值表示7:00时的存量,x=2时的y值表示8:00时的存量…依此类推.他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
| 时段 | x | 还车数(辆) | 借车数(辆) | 存量y(辆) |
| 6:00﹣7:00 | 1 | 45 | 5 | 100 |
| 7:00﹣8:00 | 2 | 43 | 11 | n |
| … | … | … | … | … |
(1)m= ,解释m的实际意义: ;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知9:00~10:00这个时段的还车数比借车数的3倍少4,求此时段的借车数.
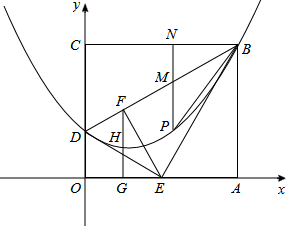
 经过B,H, D三点,求抛物线解析式;
经过B,H, D三点,求抛物线解析式;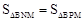 如果存在,求出点P的坐标;如果不存在,请说明理由.
如果存在,求出点P的坐标;如果不存在,请说明理由.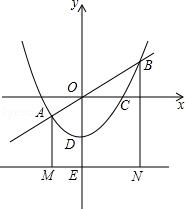
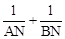 的值;
的值;
 的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(t≥0).
的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(t≥0).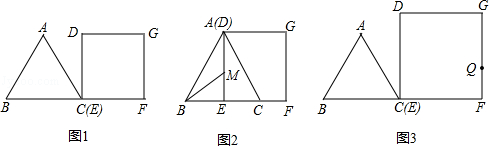
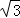 个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG﹣GD以每秒
个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG﹣GD以每秒 个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA﹣AC于P点,则是否存在t的值,使得PC⊥EQ,若存在,请求出t的值;若不存在,请说明理由.
个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA﹣AC于P点,则是否存在t的值,使得PC⊥EQ,若存在,请求出t的值;若不存在,请说明理由.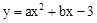 (a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
(a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
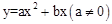 。
。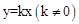 上,请用含k的代数式表示b;
上,请用含k的代数式表示b; 上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。 (k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
(k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )