题目内容
【题目】一笔总额为
元的奖金，分为一等奖、二等奖和三等奖，奖金金额均为整数，每个一等奖的奖金是每个二等奖奖金的两倍，每个二等奖的奖金是每个三等奖奖金的两倍，若把这笔奖金发给
个人，评一、二、三等奖的人数分别为
，且
，那么三等奖的奖金金额是_______元．
【答案】98或77
【解析】
由a，b，c之间的关系结合a，b，c均为整数，即可得出a，b，c的值，设三等奖的奖金金额为x元，则二等奖的奖金金额为2x元，一等奖的奖金金额为4x元，根据奖金的总额为1078元，即可得出关于x的一元一次方程，解之即可得出结论（取其为整数的值）．
解：∵a+b+c=6，0＜a≤b≤c，且a，b，c均为整数，
∴
，
，
．
设三等奖的奖金金额为x元，则二等奖的奖金金额为2x元，一等奖的奖金金额为4x元，
依题意，得：4x+2x+4x=1078，4x+2×2x+3x=1078，2×4x+2×2x+2x=1078，
解得：x=107.8（不合题意，舍去），x=98，x=77．
故答案为：98或77．
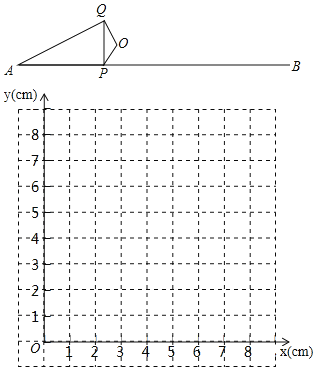
【题目】如图，P是线段AB上的一点，AB＝6cm，O是AB外一定点．连接OP，将OP绕点O顺时针旋转120°得OQ，连接PQ，AQ．小明根据学习函数的经验，对线段AP，PQ，AQ的长度之间的关系进行了探究．
下面是小明的探究过程，请补充完整：
（1）对于点P在AB上的不同位置，画图、测量，得到了线段AP，PQ，AQ的长度（单位：cm）的几组值，如表：
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PQ | 4.00 | 2.31 | 0.84 | 1.43 | 3.07 | 4.77 | 6.49 |
AQ | 4.00 | 3.08 | 2.23 | 1.57 | 1.40 | 1.85 | 2.63 |
在AP，PQ，AQ的长度这三个量中，确定 的长度是自变量， 的长度和 的长度都是这个自变量的函数；/span>
（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；
（3）结合函数图象，解决问题：当AQ＝PQ时，线段AP的长度约为 cm．
【题目】某班甲、乙、丙三名同学20天的体温数据记录如下表：
甲的体温 | 乙的体温 | 丙的体温 | ||||||||||||
温度（℃） | 36.1 | 36.4 | 36.5 | 36.8 | 温度（℃） | 36.1 | 36.4 | 36.5 | 36.8 | 温度（℃） | 36.1 | 36.4 | 36.5 | 36.8 |
频数 | 5 | 5 | 5 | 5 | 频数 | 6 | 4 | 4 | 6 | 频数 | 4 | 6 | 6 | 4 |
则在这20天中，甲、乙、丙三名同学的体温情况最稳定的是________．
