题目内容
【题目】对于平面直角坐标系xOy中的图形W1和图形W2.给出如下定义:在图形W1上存在两点A,B(点A,B可以重合),在图形W2上存在两点M,N,(点M于点N可以重合)使得AM=2BN,则称图形W1和图形W2满足限距关系
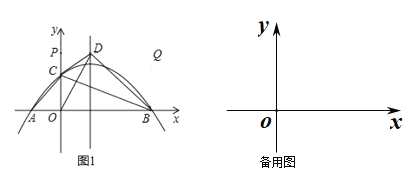
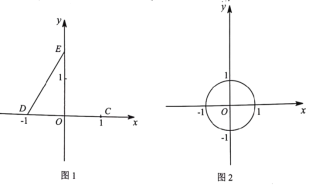
(1)如图1,点C(1,0),D(-1,0),E(0,![]() ),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.
),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.
①线段OP的最小值为_______,最大值为_______;线段CP的取值范直范围是_____;
②在点O,点C中,点____________与线段DE满足限距关系;
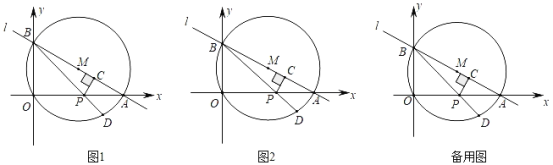
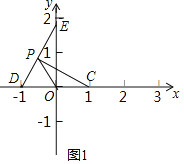
(2)如图2,⊙O的半径为1,直线![]() (b>0)与x轴、y轴分别交于点F,G.若线段FG与⊙O满足限距关系,求b的取值范围;
(b>0)与x轴、y轴分别交于点F,G.若线段FG与⊙O满足限距关系,求b的取值范围;
(3)⊙O的半径为r(r>0),点H,K是⊙O上的两个点,分别以H,K为圆心,1为半径作圆得到⊙H和K,若对于任意点H,K,⊙H和⊙K都满足限距关系,直接写出r的取值范围.
【答案】(1)①![]() ,
,![]() ,
,![]() ,②O;(2)
,②O;(2)![]() ;(3)0<r≤3.
;(3)0<r≤3.
【解析】
(1)①根据垂线段最短以及已知条件,确定OP,CP的最大值,最小值即可解决问题.②根据限距关系的定义判断即可.
(2)直线![]() 与x轴、y轴分别交于点F,G(0,b),分三种情形:①线段FG在⊙O内部,②线段FG与⊙O有交点,③线段FG 与⊙O没有交点,分别构建不等式求解即可.
与x轴、y轴分别交于点F,G(0,b),分三种情形:①线段FG在⊙O内部,②线段FG与⊙O有交点,③线段FG 与⊙O没有交点,分别构建不等式求解即可.
(3)如图3中,不妨设⊙K,⊙H的圆心在x轴上位于y轴的两侧,根据⊙H和⊙K都满足限距关系,构建不等式求解即可.
(1)①如图1中,
∵D(-1,0),E(0,![]() ),
),
∴OD=1,![]() ,
,
∴![]() ,
,
∴∠EDO=60°,
当OP⊥DE时,![]() ,此时OP的值最小,
,此时OP的值最小,
当点P与E重合时,OP的值最大,最大值为![]() ,
,
当CP⊥DE时,CP的值最小,最小值![]() ,
,
当点P与D或E重合时,PC的值最大,最大值为2,
故答案为:![]() ,
,![]() ,
,![]() .
.
②根据限距关系的定义可知,线段DE上存在两点M,N,满足OM=2ON,
故点O与线段DE满足限距关系.
故答案为O.
(2)直线![]() 与x轴、y轴分别交于点F,G(0,b),
与x轴、y轴分别交于点F,G(0,b),
当0<b<1时,线段FG在⊙O内部,与⊙O无公共点,
此时⊙O上的点到线段FG的最小距离为1-b,最大距离为1+b,
∵线段FG与⊙O满足限距关系,
∴1+b≥2(1-b),
解得![]() ,
,
∴b的取值范围为![]() .
.
当1≤b≤2时,线段FG与⊙O有公共点,线段FG与⊙O满足限距关系,
当b>2时,线段FG在⊙O的外部,与⊙O没有公共点,
此时⊙O上的点到线段FG的最小距离为![]() ,最大距离为b+1,
,最大距离为b+1,
∵线段FG与⊙O满足限距关系,
∴![]() ,
,
而![]() 总成立,
总成立,
∴b>2时,线段FG 与⊙O满足限距关系,综上所述,b的取值范围为![]() .
.
(3)如图3中,不妨设⊙K,⊙H的圆心在x轴上位于y轴的两侧,
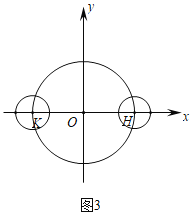
两圆的距离的最小值为2r-2,最大值为2r+2,
∵⊙H和⊙K都满足限距关系,
∴2r+2≥2(2r-2),
解得r≤3,
故r的取值范围为0<r≤3.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】某大学为了解学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行了评分,统计如下:
人数 满意度评分 餐厅 | 非常满意 | 较满意 | 一般 | 不太满意 | 非常不满意 | 合计 |
A | 28 | 40 | 10 | 10 | 12 | 100 |
B | 25 | 20 | 45 | 6 | 4 | 100 |
若小芸要在A,B两家餐厅中选择一家用餐,根据表格中数据,你建议她去_____餐厅(填A或B),理由是_____.