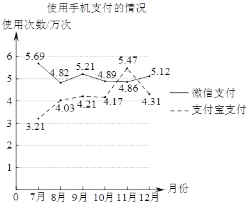题目内容
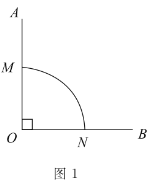
【题目】已知:![]() 为等边三角形.
为等边三角形.
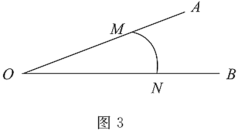
(1)求作:![]() 的外接圆
的外接圆![]() .(不写作法,保留作图痕迹)
.(不写作法,保留作图痕迹)
(2)射线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 的切线
的切线![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() .
.
①根据题意,将(1)中图形补全;
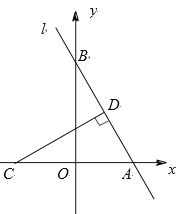
②求证:![]() ;
;
③若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)①见解析;②见解析;③EF=![]() .
.
【解析】
(1)直接利用外接圆的作法作出三角形任意两边的垂直平分线,进而得出外接圆圆心,进而得出答案;
(2)①按题意画出图形即可;
②连接OB,OC,证明AE⊥BC.可得出AE⊥EF,则结论得证;
③得出∠BOD=60°,设OD=x,则OB=OE=2+x,得出cos∠BOD=![]() ,求出x=2,得出tan∠BAD=
,求出x=2,得出tan∠BAD=![]() ,则可求出EF的值.
,则可求出EF的值.
解:(1)如图所示:⊙O即为所求.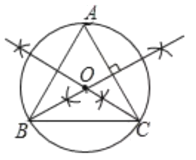
(2)①如图,补全图形: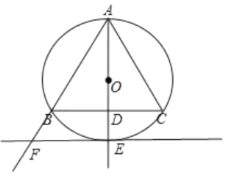
②证明:连接OB,OC,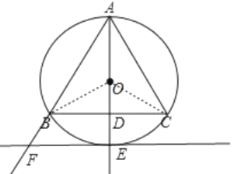
∵OB=OC,
∴点O在线段BC的垂直平分线上,
∵△ABC为等边三角形,
∴AB=AC,
∴点A在线段BC的垂直平分线上,
∴AO垂直平分BC,
∴AE⊥BC.
∵直线EF为⊙O的切线,
∴AE⊥EF,
∴EF∥BC;
③∵△ABC为等边三角形,
∴∠BAC=60°,
∵AB=AC,AE⊥BC,
∴∠BAD=![]() ∠BAC,
∠BAC,
∴∠BAD=30°,
∴∠BOD=60°,
∵DE=2,
设OD=x,
∴OB=OE=2+x,
在Rt△OBD中,∵OD⊥BC,∠BOD=60°,
∴cos∠BOD=![]() ,
,
∴x=2,
∴OD=2,OB=4,
∴AE=8,
在△AEF中,∵AE⊥EF,∠BAD=30°,
∴tan∠BAD=![]() ,
,
∴EF=![]() .
.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案【题目】北京某超市按月订购一种酸奶,每天的进货量相同.根据往年的销售经验,每天需求量与当天最高气温(单位:℃)有关.为了确定今年六月份的酸奶订购计划,对前三年六月份的最高气温及该酸奶需求量数据进行了整理、描述和分析,下面给出了部分信息.
a.酸奶每天需求量与当天最高气温关系如表:
最高气温t(单位:℃) | 20≤t<25 | 25≤t<30 | 30≤t≤40 |
酸奶需求量(单位:瓶/天) | 300 | 400 | 600 |
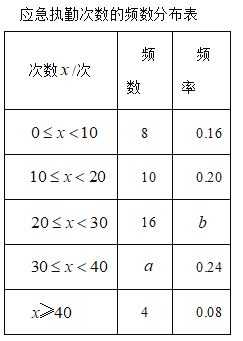
b.2017年6月最高气温数据的频数分布统计表如表(不完整):
2017年6月最高气温数据的频数分布表:
分组 | 频数 | 频率 |
20≤t<25 | 3 | |
25≤t<30 | m | 0.20 |
30≤t<35 | 14 | |
35≤t≤40 | 0.23 | |
合计 | 30 | 1.00 |
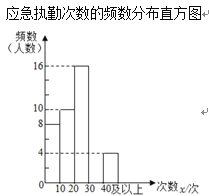
c.2018年6月最高气温数据的频数分布直方图如图:
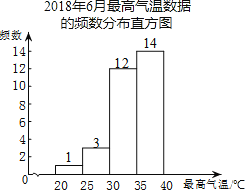
d.2019年6月最高气温数据如下(未按日期顺序):
25 26 28 29 29 30 31 31 31 32 32 32 32 32 32
33 33 33 33 33 34 34 34 35 35 35 35 36 36 36
根据以上信息,回答下列问题:
(1)m的值为 ;
(2)2019年6月最高气温数据的众数为 ,中位数为 ;
(3
(4)已知该酸奶进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.
①2019年6月这种酸奶每天的进货量为500瓶,则此月这种酸奶的利润为 元;
②根据以上信息,预估2020年6月这种酸奶订购的进货量不合理的为 .
A.550瓶/天
B.600瓶/天
C.380瓶/天