题目内容
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() .
.
(1)抛物线的对称轴为_______;
(2)若当![]() 时,
时,![]() 的最小值是
的最小值是![]() ,求当
,求当![]() 时,
时,![]() 的最大值;
的最大值;
(3)已知直线![]() 与抛物线
与抛物线![]() 存在两个交点,设左侧的交点为点
存在两个交点,设左侧的交点为点![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() ,即
,即![]() 的最大值是
的最大值是![]() ;(3)
;(3)![]()
【解析】
(1)根据抛物线的对称轴公式即可得结论;
(2)根据抛物线的对称轴为x=2,可得顶点在1≤x≤5范围内,和y的最小值是-1,得顶点坐标为(2,-1),把顶点(2,-1)代入y=ax2-4ax+1,可得a的值,进而可得y的最大值;
(3)当x=-2时,P(-2,5),把P(-2,5)代入y=ax2-4ax+1,当x1=-1时,P(-1,4),把P(-1,4)代入y=ax2-4ax+1,分别求出a的值,再根据函数的性质即可得a的取值范围.
(1)抛物线的对称轴为:![]() ,
,
故答案为:x=2;
(2)解:∵抛物线的对称轴为x=2,
∴顶点在1≤x≤5范围内,
∵y的最小值是-1,
∴顶点坐标为(2,-1).
∵a>0,开口向上,
∴当x>2时,y随x的增大而增大,
即x=5时,y有最大值,
∴把顶点(2,-1)代入y=ax2-4ax+1,
∴4a-8a+1=-1,
解得![]()
∴![]()
∴当x=5时,![]()
即y的最大值是![]() ;
;
(3)当x=-2时,P(-2,5),
把P(-2,5)代入y=ax2-4ax+1,
∴4a+8a+1=5,
解得a=![]() ,
,
当x1=-1时,P(-1,4),
把P(-1,4)代入y=ax2-4ax+1,
∴a+4a+1=4,
解得a=![]() ,
,
∴![]() ≤a<
≤a<![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】如图1,四边形ABCD为矩形,曲线L经过点D.点Q是四边形ABCD内一定点,点P是线段AB上一动点,作PM⊥AB交曲线L于点M,连接QM.
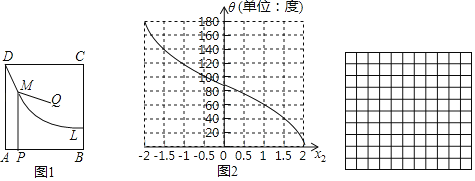
小东同学发现:在点P由A运动到B的过程中,对于x1=AP的每一个确定的值,θ=∠QMP都有唯一确定的值与其对应,x1与θ的对应关系如表所示:
x1=AP | 0 | 1 | 2 | 3 | 4 | 5 |
θ=∠QMP | α | 85° | 130° | 180° | 145° | 130° |
小芸同学在读书时,发现了另外一个函数:对于自变量x2在﹣2≤x2≤2范围内的每一个值,都有唯一确定的角度θ与之对应,x2与θ的对应关系如图2所示:
根据以上材料,回答问题:
(1)表格中α的值为 .
(2)如果令表格中x1所对应的θ的值与图2中x2所对应的θ的值相等,可以在两个变量x1与x2之间建立函数关系.
①在这个函数关系中,自变量是 ,因变量是 ;(分别填入x1和x2)
②请在网格中建立平面直角坐标系,并画出这个函数的图象;
③根据画出的函数图象,当AP=3.5时,x2的值约为 .