题目内容
如图,已知PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.
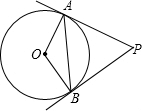
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.

(1)求∠APB的度数;
(2)当OA=3时,求AP的长.
(1)60°;(2)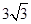 .
.
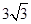 .
.试题分析:(1)根据四边形的内角和为360°,根据切线的性质可知:∠OAP=∠OBP=90°,求出∠AOB的度数,可将∠APB的度数求出;
(2)作辅助线,连接OP,在Rt△OAP中,利用三角函数,可将AP的长求出.
试题解析:(1)∵在△ABO中,OA=OB,∠OAB=30°,
∴∠AOB=180°-2×30°=120°,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°,
∴在四边形OAPB中,
∠APB=360°-120°-90°-90°=60°.
(2)如图,连接OP;
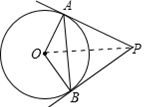
∵PA、PB是⊙O的切线,
∴PO平分∠APB,即∠APO=
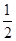 ∠APB=30°,
∠APB=30°,又∵在Rt△OAP中,OA=3,∠APO=30°,
∴AP=
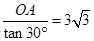 .
. 考点: 切线的性质.

练习册系列答案
相关题目
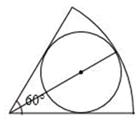
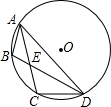
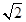 与⊙O的位置关系是( )
与⊙O的位置关系是( )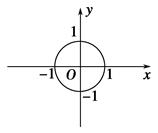
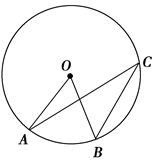
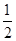 B.
B.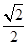
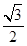 D.
D.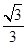
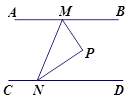
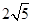 为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为
为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为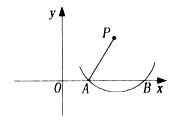
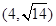
 )
)