题目内容
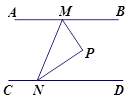
如图,动点M、N分别在直线AB与CD上,且AB∥CD,∠BMN与∠MND的角平分线相交于点P,若以MN为直径作⊙O,则点P与⊙0的位置关系是 ( ) .

| A.点P在⊙O外 | B.点P在⊙O内 |
| C.点P在⊙0上 | D.以上都有可能 |
C.
试题分析:∵AB∥CD,
∴∠BMN+∠MND=180°,
∵∠BMN与∠MND的平分线相交于点P,
∴∠PMN=
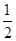 ∠BMN,∠PNM=
∠BMN,∠PNM=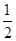 ∠MND,
∠MND,∴∠PMN+∠PNM=90°,
∴∠MPN=180°-(∠PMN+∠PNM)=180°-90°=90°,
∴以MN为直径作⊙O时,OP=
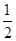 MN=⊙O的半径,
MN=⊙O的半径,∴点P在⊙O上.
故选C.
考点: 点与圆的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
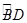 的中点,CE⊥AB于点E,BD交CE于点F.
的中点,CE⊥AB于点E,BD交CE于点F.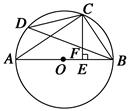
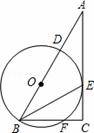
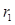 =2、
=2、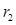 =4,若⊙O1与⊙O2的圆心距
=4,若⊙O1与⊙O2的圆心距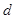 =5.则⊙O1与⊙O2的位置关系是___________.
=5.则⊙O1与⊙O2的位置关系是___________.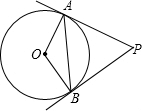
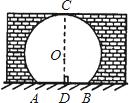
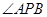 =
=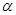 ,∠AQB=
,∠AQB=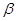 ,则
,则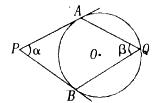
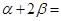 90° B.
90° B. 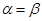 C.
C. 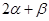 =180° D.
=180° D.