题目内容
作图题(写出作法,保留作图痕迹):
M、N为△ABC为AB、AC上的两个定点,请你在BC边上找一点P,使四边形AMPN周长最小?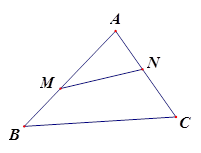
M、N为△ABC为AB、AC上的两个定点,请你在BC边上找一点P,使四边形AMPN周长最小?

解:作法:
(1)作M关于BC的对称点M’
(2)连结M’N交BC于P点
(3)连线MP,则△PMN周长最小P为所求作的点,
此时,四边形AMPN的周长最小。
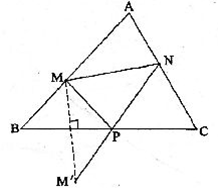
(1)作M关于BC的对称点M’
(2)连结M’N交BC于P点
(3)连线MP,则△PMN周长最小P为所求作的点,
此时,四边形AMPN的周长最小。

分析:由于四边形AMPN周长=AM+PM+PN+AN,而AM和AN是定值,故只需在BC上找一点P,使PM+PN最小。如果设M关于BC的对称点为M’使PM’+PN最小。
解答:
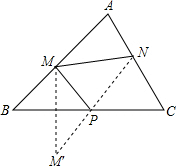
作法:
(1)作M关于BC的对称点M’
(2)连接M’N交BC于P点
(3)连线MP,则△PMN周长最小P为所求作的点,此时,四边形AMPN的周长最小。
点评:本题考查了轴对称中最短路线问题,解这类问题的关键是把两条线段的和转化为一条线段,运用四角形边的关系解决。

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目

 的周长是18cm,
的周长是18cm, <
< .对角线
.对角线 、
、 相交于点
相交于点 ,若
,若 与
与 的周长差是5cm,则边
的周长差是5cm,则边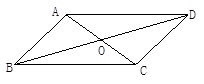


 .
.