题目内容
【题目】已知：∠BAC．
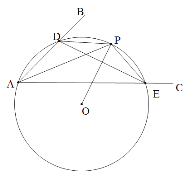
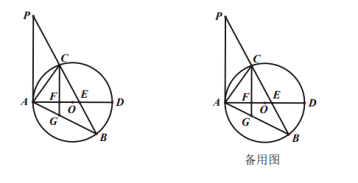
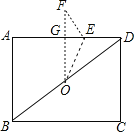
（1）如图，在平面内任取一点O；
（2）以点O为圆心，OA为半径作圆，交射线AB于点D，交射线AC于点E；
（3）连接DE，过点O作线段DE的垂线交⊙O于点P；
（4）连接AP，DP和PE．根据以上作图过程及所作图形，下列四个结论中：
①△ADE是⊙O的内接三角形； ② 
；
③ DE=2PE； ④ AP平分∠BAC．
所有正确结论的序号是______________．
【答案】①④
【解析】
①按照圆的内接三角形的定义判断即可，三顶点都在一个圆周上的三角形，叫做这个圆周的内接三角形；
② 利用垂径定理得到弧长之间的关系即可；
③设OP与DE交于点M，利用垂径定理可得DE⊥OP，DE=2ME，再利用直角三角形中斜边长大于直角边，找到PE与与ME的关系，进一步可以得到DE与PE的关系；
④根据
，即可得到∠DAP=∠PAE，则AP平分∠BAC．
解：①点A、D、E三点均在⊙O上，所以△ADE是⊙O的内接三角形，此项正确；
② ∵DE⊥DE交⊙O于点P
∴
并不能证明
与
、
关系，
∴
不正确；
③设OP与DE交于点M
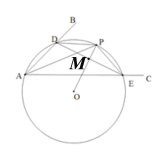
∵DE⊥DE交⊙O于点P
∴DE⊥OP， ME=
DE（垂径定理）
∴△PME是直角三角形
∴ME＜PE
∴
＜PE
∴DE＜2PE
故此项错误.
④∵ （已证）
∴∠DAP=∠PAE（同弧所对的圆周角相等）
∴AP平分∠BAC．
故此项正确.
故正确的序号为：①④
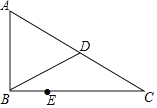
通城学典默写能手系列答案
【题目】如图1，线段AB及一定点C、P是线段AB上一动点，作直线CP，过点A作AQ⊥CP于点Q，已知AB＝7cm，设A、P两点间的距离为xcm，A、Q两点间的距离为y1cm，P、Q两点间的距离为y2cm．小明根据学习函数的经验，分别对函数y1、y2随自变量x的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整：
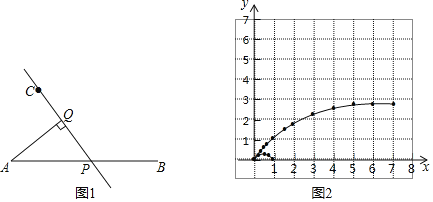
（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了y1、y2与x的几组对应值．
x/cm | 0 | 0.3 | 0.5 | 0.8 | 1 | 1.5 | 2 | 3 | 4 | 5 | 6 | 7 |
y1/cm | 0 | 0.28 | 0.49 | 0.79 | 1 | 1.48 | 1.87 | 2.37 | 2.61 | 2.72 | 2.76 | 2.78 |
y2/cm | 0 | 0.08 | 0.09 | 0.06 | 0 | 0.29 | 0.73 | 1.82 |
| 4.20 | 5.33 | 6.41 |
（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），（x，y2），并画出函数y1，y2的图象；
（3）结合函数图象，解决问题：当△APQ中有一个角为30°时，AP的长度约为 cm．
