题目内容
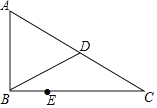
【题目】在Rt△ABC中,∠ABC=90°,∠C=30°,AC=8,BD为边AC上的中线,点E在边BC上,且BE:BC=3:8,点P在Rt△ABC的边上运动,当PD:AB=1:2时,EP的长为_____.
【答案】![]() 或
或![]() 或
或![]()
【解析】
根据直角三角形的性质得到AB![]() AC=4,BC=4
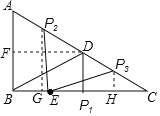
AC=4,BC=4![]() ,∠A=60°,过D作DF⊥AB于F,则DF∥BC,由直角三角形的性质得到AD=CD=BD,得到DF的长,当PD:AB=1:2时,点P在AC和BC上,然后分三种情况讨论:①当点P在BC上,②当P点在线段AD上时,③当P点在线段CD上时.
,∠A=60°,过D作DF⊥AB于F,则DF∥BC,由直角三角形的性质得到AD=CD=BD,得到DF的长,当PD:AB=1:2时,点P在AC和BC上,然后分三种情况讨论:①当点P在BC上,②当P点在线段AD上时,③当P点在线段CD上时.
∵在Rt△ABC中,∠ABC=90°,∠C=30°,AC=8,∴AB![]() AC=4,BC=4
AC=4,BC=4![]() ,∠A=60°.
,∠A=60°.
∵PD:AB=1:2,∴PD=2.
过D作DF⊥AB于F,则DF∥BC.
∵BD为边AC上的中线,∴AD=CD=BD,∴AF=BF,∴DF=2![]() .
.
∵点P在Rt△ABC的边上运动,PD=2<2![]() ,∴当PD:AB=1:2时,点P在AC和BC上.
,∴当PD:AB=1:2时,点P在AC和BC上.
①当点P在BC上.
∵PD=2![]() AB,∴P为BC的中点,∴BP
AB,∴P为BC的中点,∴BP![]() BC=2
BC=2![]() .
.
∵BE:BC=3:8,∴BE![]() ,∴EP=BP﹣BE
,∴EP=BP﹣BE![]() ;
;
②当P点在线段AD上时.
∵PD=2,AD=4,∴P为AD的中点,∴AP=2,过P作PG⊥BC于G,∴PG∥AB,∴△CPG∽△CAB,∴![]() ,∴
,∴![]() ,∴PG=3,CG=3
,∴PG=3,CG=3![]() ,∴GE
,∴GE![]() ,∴PE
,∴PE![]() ;
;
③当P点在线段CD上时.
∵PD=2,CD=4,∴PC=2,过P作PH⊥BC于H,∴PH=1,CH![]() ,∴EH
,∴EH![]() ,∴PE
,∴PE![]() .
.
综上所述:EP的长为![]() 或
或![]() 或
或![]() .
.
故答案为:![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目