Question

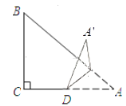
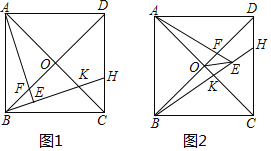
【题目】如图1，正方形ABCD中，对角线AC与BD交于点O，H为CD边上一点，连接BH交AC于K；E为BH上一点，连接AE交BD于F．

（1）若AE⊥BH于E，且CK＝，AD＝6，求AF的长；

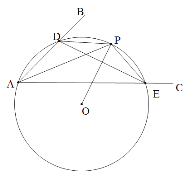
（2）如图2，若AB＝BE，且∠BEO＝∠EAO，求证：AE＝2OE．

Answer 1

【答案】（1）AF的长为；（2）证明见解析．

【解析】

（1）根据正方形的性质及AE⊥BH于E，及对顶角相等等条件证得△BOK≌△AOF，故OK＝OF，再利用已知线段的长和勾股定理，即可求得AF．

（2）过O作OM⊥OE，交AE于点M，连接BM，先证△OME为等腰直角三角形，再证BM⊥AE，然后利用等腰三角形的三线合一性质求得AM＝ME，最后利用ME＝OE及AE和ME的数量关系．即可证明．

解：（1）∵四边形ABCD是正方形

∴AC＝BD，AC⊥BD

∴AO＝BO，∠AOB＝∠BOC＝90°

∵AE⊥BH

∴∠AEB＝90°

∵∠AFO＝∠BFE

∴∠OAF＝∠OBK

∴△BOK≌△AOF

∴OK＝OF

∵AD＝6

∴AC＝AD＝6，AO＝CO＝3

∴OK＝OF＝CO﹣CK＝2

∴AF＝＝．

∴AF的长为．

（2）证明：过O作OM⊥OE，交AE于点M，连接BM

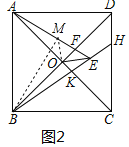
∵AB＝BE

∴∠BAM＝∠BEA

∵∠EAO＝∠BEO

∴∠BAO＝∠MEO＝45°

∴△OME为等腰直角三角形

∴OE＝OM

∵∠AOB＝∠MOE＝90°

∴∠BOM＝∠AOE

又∵OM＝OE，AO＝BO

∴△BOM≌△AOE

∴∠AEO＝∠BMO＝45°

∴∠BME＝∠BMO＋∠OME＝∠AEO＋∠OME＝90°

∴BM⊥AE

∵AB＝BE

∴AM＝ME

∵ME＝OE

∴AE＝2OE．