题目内容
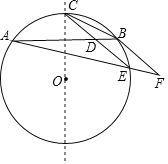
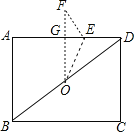
【题目】如图，在矩形ABCD中，AB=6，BC=8，点O为对角线BD的中点，点E为边AD上一点，连接OE，将△DOE沿OE翻折得到△OEF，若OF⊥AD于点G，则OE=______．
【答案】
【解析】
由矩形的性质和勾股定理得出BD=
=10，得出OD=5，由折叠的性质得：∠F=∠ADB，OF=OD=5，证出OG是△ABD的中位线，△GEF∽△ABD，得出OG=
AB=3，
=
，求出GE=
，在Rt△OGE中，由勾股定理即可得出结果．
解：∵四边形ABCD是矩形，
∴∠A=90°，AD=BC=8，
∴AB⊥AD，BD==10，
∵点O为对角线BD的中点，
∴OD=5，
由折叠的性质得：∠F=∠ADB，OF=OD=5，
∵OF⊥AD，∴OF∥AB，∠OGE=∠FGE=90°=∠A，
∴OG是△ABD的中位线，△GEF∽△ABD，
∴OG=AB=3，=，
∴FG=OF-OG=2，
=
，
∴GE=，
在Rt△OGE中，由勾股定理得：OE=
=
=
；
故答案是：．
练习册系列答案
相关题目
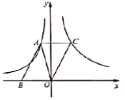
【题目】设函数y=k1x+
，且k1k2≠0，自变量x与函数值y满足以下表格：
x | …… | -4 | -3 | -2 | -1 | - |
| 1 | 2 | 3 | 4 | …… |
y | …… | -3 | -2 | -1 | 0 | 1 | -1 | 0 | 1 | m | n | …… |
（1）根据表格直接写出y与x的函数表达式及自变量x的取值范围______
（2）补全上面表格：m=______，n=______；在如图所示的平面直角坐标系中，请根据表格中的数据补全y关于x的函数图象；
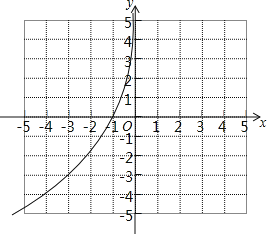
（3）结合函数图象，解决下列问题：
①写出函数y的一条性质：______；
②当函数值y≥
时，x的取值范围是______；
③当函数值y=-x时，结合图象请估算x的值为______（结果保留一位小数）
