题目内容
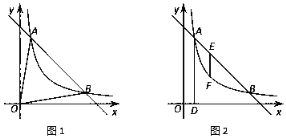
【题目】![]() 问题发现
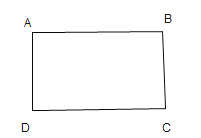
问题发现
如图![]() ,正方形
,正方形![]() 将正方形
将正方形![]() 绕点
绕点![]() 旋转,直线
旋转,直线![]() 交于点
交于点![]() 请直接写出线段
请直接写出线段![]() 与
与![]() 的数量关系是 ,位置关系是 _;
的数量关系是 ,位置关系是 _;
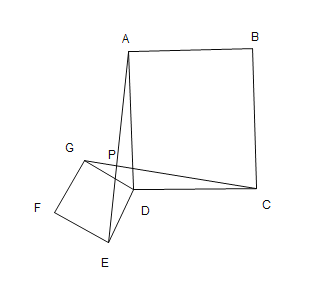
![]() 拓展探究
拓展探究
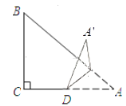
如图![]() ,矩形
,矩形![]() 将矩形
将矩形![]() 绕点
绕点![]() 旋转,直线
旋转,直线![]() 交于点
交于点![]()
![]() 中线段关系还成立吗/若成立,请写出理由;若不成立,请写出线段
中线段关系还成立吗/若成立,请写出理由;若不成立,请写出线段![]() 的数量关系和位置关系,并说明理由;
的数量关系和位置关系,并说明理由;
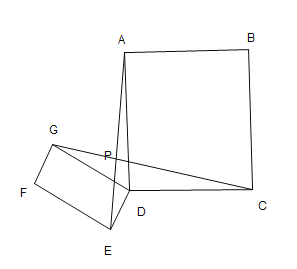
![]() 解决问题
解决问题
在![]() 的条件下,
的条件下,![]() 矩形
矩形![]() 绕
绕![]() 点旋转过程中,请直接写出当点
点旋转过程中,请直接写出当点![]() 与点
与点![]() 重合时,线段
重合时,线段![]() 的长,
的长,
【答案】![]() ;
;![]() 中数量关系不成立,位置关系成立.
中数量关系不成立,位置关系成立.![]() ,理由见解析;
,理由见解析;![]() 或
或![]()
【解析】
(1)证明△ADE≌△CDG(SAS),可得AE=CG,∠DAG=∠DCG,再由直角三角形两个锐角互余即可证得AE⊥CG;
(2)先证明△ADE∽△CDG,利用相似三角形的性质证明即可.
(3)先通过作图找到符合题意的两种情况,第一种情况利用勾股定理求解即可;第二种情况借助相似三角形及勾股定理计算即可.
(1)![]() ;
;
理由如下:由题意知在正方形![]() 中,
中,
![]() ,
,![]() ,
,
![]()
![]()
在△ADE与△CDG中,
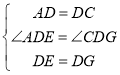
∴△ADE≌△CDG(SAS)
∴![]() ,
,![]()
∵对顶角相等,
∴![]()
![]()
![]() .
.
(2)(1)中数量关系不成立,位置关系成立.即:![]()
理由如下:
由题意知在矩形![]() 中,
中,![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,![]()
∵对顶角相等
∴![]()
![]()
![]() .
.
综上所述:![]()
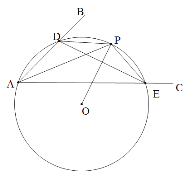
(3)
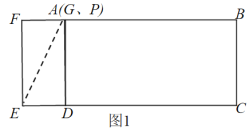
如图1,当点G、P在点A处重合时,连接AE,
则此时∠ADE=∠GDE=90°
∴在Rt△ADE中,AE=![]() ,
,
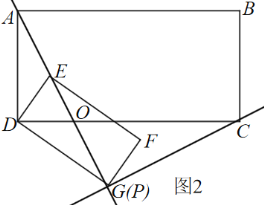
如图1,当点G、P重合时, 则点A、E、G在同一直线上,
∵AD=DG=4,
∴∠DAG=∠DGA,
∵∠ADC=∠AGP=90°,∠AOD=∠COG,
∴∠DAG=∠COG,
∴∠DGA=∠COG,
又∵∠GDO=∠CDG,
∴△GDO∽△CDG,
∴![]()
∴![]()
∴DO=2,CG=2OG,
∴OC=DC-DO=8-2=6,
∵在Rt△COG中,OG2+GC2=OC2,
∴OG2+(2OG)2=62,
∴OG=![]() (舍负),
(舍负),
∴CG=![]() ,
,
由(2)得:![]()
∴AE=![]() ,
,
综上所述,AE的长为![]() 或
或![]() .
.

【题目】2019年中国北京世界园艺博览会已于2019年4月29日在北京市延庆区开展,吸引了大批游客参观游览.五一小长假期间平均每天入园人数大约是8万人,佳佳等5名同学组成的学习小组,随机调查了五一假期中入园参观的部分游客,获得了他们在园内参观所用时间,并对数据进行整理,描述和分析,下面给出了部分信息:
a.参观时间的频数分布表如下:
时间 | 频数(人数) | 频率 |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
合计 |
| 1.000 |
b.参观时间的频数分布直方图如图:
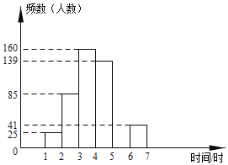
根据以上图表提供的信息,解答下列问题:
(1)这里采用的调查方式是 ;
(2)表中![]() ,
,![]() ,
,![]() ;
;
(3)并请补全频数分布直方图;
(4)请你估算五一假期中平均每天参观时间小于4小时的游客约有多少万人?