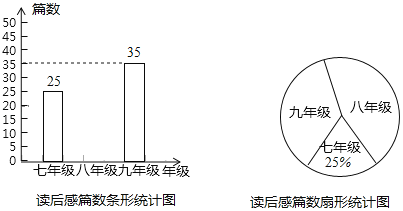
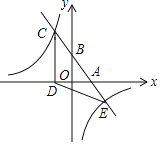
题目内容
【题目】在平面直角坐标系xOy中,将抛物线![]() (m≠0)向右平移
(m≠0)向右平移![]() 个单位长度后得到抛物线G2,点A是抛物线G2的顶点.
个单位长度后得到抛物线G2,点A是抛物线G2的顶点.
(1)直接写出点A的坐标;
(2)过点(0,![]() )且平行于x轴的直线l与抛物线G2交于B,C两点.
)且平行于x轴的直线l与抛物线G2交于B,C两点.
①当∠BAC=90°时.求抛物线G2的表达式;
②若60°<∠BAC<120°,直接写出m的取值范围.
【答案】(1)(![]() ,2
,2![]() );(2)①y=
);(2)①y=![]() (x-
(x-![]() )2+2
)2+2![]() ;②
;②![]()
【解析】
(1)先求出平移后是抛物线G2的函数解析式,即可求得点A的坐标;
(2)①由(1)可知G2的表达式,首先求出AD的值,利用等腰直角的性质得出BD=AD=![]() ,从而求出点B的坐标,代入即可得解;
,从而求出点B的坐标,代入即可得解;
②分别求出当∠BAC=60°时,当∠BAC=120°时m的值,即可得出m的取值范围.
(1)∵将抛物线G1:y=mx2+2![]() (m≠0)向右平移
(m≠0)向右平移![]() 个单位长度后得到抛物线G2,
个单位长度后得到抛物线G2,
∴抛物线G2:y=m(x-![]() )2+2
)2+2![]() ,
,
∵点A是抛物线G2的顶点.
∴点A的坐标为(![]() ,2
,2![]() ).
).
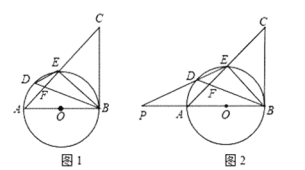
(2)①设抛物线对称轴与直线l交于点D,如图1所示.
∵点A是抛物线顶点,
∴AB=AC.
∵∠BAC=90°,
∴△ABC为等腰直角三角形,
∴CD=AD=![]() ,
,
∴点C的坐标为(2![]() ,
,![]() ).
).
∵点C在抛物线G2上,
∴![]() =m(2
=m(2![]() -
-![]() )2+2
)2+2![]() ,
,
解得:![]() .
.
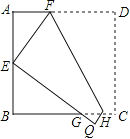
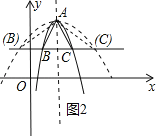
②依照题意画出图形,如图2所示.
同理:当∠BAC=60°时,点C的坐标为(![]() +1,
+1,![]() );
);
当∠BAC=120°时,点C的坐标为(![]() +3,
+3,![]() ).
).
∵60°<∠BAC<120°,
∴点(![]() +1,
+1,![]() )在抛物线G2下方,点(
)在抛物线G2下方,点(![]() +3,
+3,![]() )在抛物线G2上方,
)在抛物线G2上方,
∴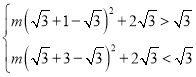 ,
,
解得:![]() .
.


练习册系列答案
相关题目