题目内容
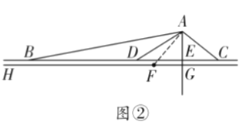
【题目】如图,某海监船向正西方向航行,在A处望见一艘正在作业的渔船D在南偏西45°方向,海监船航行到B处时,望见渔船D在南偏东45°方向,又航行半小时到达C处望见渔船D在南偏东62°方向,若海监船的速度为40海里/小时,求A、B之间的距离.(精确到0.1海里,参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
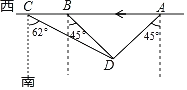
【答案】A、B之间的距离为45.5海里.
【解析】
过点D作DE⊥AB于点E,设DE=x海里,在Rt△CDE中表示出CE,在Rt△BDE中表示出BE,再由CB=20海里,可得出关于x的方程,解出后即可计算AB的长度.
过点D作DE⊥AB于点E,
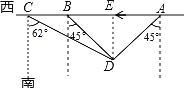
∵∠ADE=∠BDE=45°,
∴AE=BE=DE,
设DE=x海里,则BE=x海里,
∵BC=![]() ,
,
∴CE=x+20,
在Rt△CDE中,∠CDE=62°,
![]() ,
,
∴![]() ,
,
∴x=![]() ≈22.73,
≈22.73,
∴AB=2x=2×22.73≈45.5,
答:A、B之间的距离为45.5海里.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目