题目内容
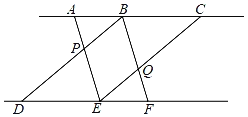
【题目】如图,已知AC∥DF,点B在AC上,点E在DF上,连结AE,BD相交于点P,连结CE,BF相交于点Q,若AB=EF,BC=DE.
(1)求证:四边形BPEQ为平行四边形;
(2)若DP=2BP,BF=3,CE=6.求证:四边形BPEQ为菱形.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)证出四边形ABFE和四边形BCED是平行四边形,得出AE=BF,AE∥BF,BD∥CE,即可得出结论;
(2)由平行四边形的性质得出AE=BF=3,BD=CE=6,求出QE=BP=![]() BD=2,证得△APB∽△EPD,求出EP=
BD=2,证得△APB∽△EPD,求出EP=![]() AE=2,得出BP=EP,即可得出结论.
AE=2,得出BP=EP,即可得出结论.
(1)∵AC∥DF,AB=EF,BC=DE,
∴四边形ABFE和四边形BCED都是平行四边形,
∴AE∥BF,BD∥CE,
∴四边形BPEQ为平行四边形;
(2)由(1)得:四边形ABFE、四边形BCED和四边形BPEQ为平行四边形,
∴AE=BF=3,BD=CE=6,
∵DP=2BP,
∴QE=BP=![]() BD=2,
BD=2,
∵AC∥DF,
∴△APB∽△EPD,
∴![]() =
=![]() =
=![]() ,
,
∴EP=![]() AE=2,
AE=2,
∴BP=EP,
∴四边形BPEQ为菱形.

练习册系列答案
相关题目