题目内容
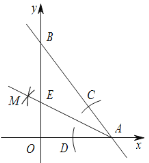
【题目】如图,直线y![]() x4与 x轴、y轴的交点为A,B.按以下步骤作图:
x4与 x轴、y轴的交点为A,B.按以下步骤作图:
①以点 A 为圆心,适当长度为半径作弧,分别交 AB,x 轴于点 C,D;
②分别以点 C,D 为圆心,大于![]() CD的长为半径作弧,两弧在∠OAB内交于点M;③作射线AM,交 y 轴于点E.则点 E 的坐标为____________
CD的长为半径作弧,两弧在∠OAB内交于点M;③作射线AM,交 y 轴于点E.则点 E 的坐标为____________
【答案】(0,![]() )
)
【解析】
过点E作EF⊥AB于F,根据直线解析式求出A、B的坐标,根据勾股定理得AB=5,再通过证明△OAE≌△FAE,可得OA=AF=3,故BF=AB-AF=2,设OE=x,则EF=x,BE=4-x,根据勾股定理列方程求解即可.
解:过点E作EF⊥AB于F,如图所示,
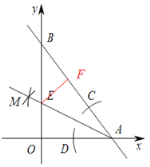
在y![]() x4中,当x=0时,y=4;当y=0时,x=3,
x4中,当x=0时,y=4;当y=0时,x=3,
即A(3,0),B(0,4),
在Rt△AOB中,由勾股定理得:AB=5,
由题意的尺规作图方法可知,AM为∠BOA的平分线,
∴EO=EF,
∴△OAE≌△FAE,
∴OA=AF=3,
∴BF=AB-AF=2,
设OE=x,则EF=x,BE=4-x,
在Rt△BEF中,由勾股定理得:
(4-x)2=x2+22,
解得:x=![]() ,即OE=
,即OE=![]() ,
,
∴答案为:(0,![]() ).
).

练习册系列答案
相关题目