题目内容
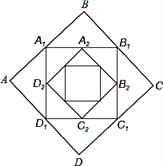
【题目】如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,由顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第六个正方形A6B6C6D6周长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据题意,利用中位线定理可证明顺次连接正方形ABCD四边中点得正方形![]() 的面积为正方形ABCD面积的一半,根据面积关系可得周长关系,以此类推可得正方形
的面积为正方形ABCD面积的一半,根据面积关系可得周长关系,以此类推可得正方形![]() 的周长.
的周长.
本题解析: 顺次连接正方形ABCD四边的中点得正方形![]() ,则得正方形
,则得正方形![]() 的面积为正方形ABCD面积的一半,即
的面积为正方形ABCD面积的一半,即![]() ,则周长是原来的
,则周长是原来的![]() ;
;
顺次连接正方形![]() 中点得正方形
中点得正方形![]() ,则正方形
,则正方形![]() 的面积为正方形
的面积为正方形![]() 面积的一半,即
面积的一半,即![]() ,则周长是原来的
,则周长是原来的![]() ;
;
顺次连接正方形![]() 得正方形
得正方形![]() ,则正方形
,则正方形![]() 的面积为正方形
的面积为正方形![]() 面积的一半,即
面积的一半,即![]() ,则周长是原来的
,则周长是原来的![]() ;
;
顺次连接正方形![]() 中点得正方形
中点得正方形![]() ,则正方形
,则正方形![]() 的面积为正方形
的面积为正方形![]() 面积的一半
面积的一半![]() ,则周长是原来的
,则周长是原来的![]() ;
;
…
故第n个正方形周长是原来的![]() ,
,
以此类推:第六个正方形![]() 周长是原来的
周长是原来的![]() ,
,
∵正方形ABCD的边长为1,
∴周长为4,
∴第六个正方形A6B6C6D6周长是![]() .
.
故答案为![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目