��Ŀ����
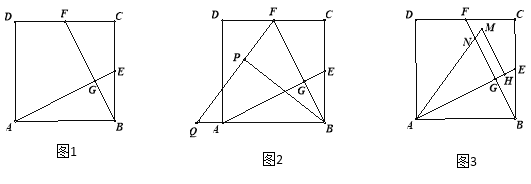
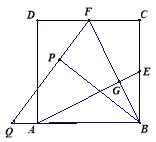
����Ŀ����ͼ1����������ABCD�У�E��F�ֱ�ΪBC��CD���е㣬����AE��BF������ΪG��
(1)��֤��AE��BF��
(2)����BCF��BF���ۣ��õ���BPF����ͼ2�����ӳ�FP��BA���ӳ����ڵ�Q����sin��BQP��ֵ��
(3)����ABE�Ƶ�A��ʱ�뷽����ת��ʹ��AB��������AE�ϣ��õ���AHM����ͼ3������AM��BF�ཻ�ڵ�N����������ABCD���߳�Ϊ4ʱ��ֱ��д���ı���GHMN�������
���𰸡���1��֤����������2��![]() ��3��
��3��![]()
��������
�����������1������Rt��ABE��Rt��BCF�������ýǵĹ�ϵ�����BGE=90����֤��
��2����BCF��BF���ۣ��õ���BPF�����ýǵĹ�ϵ���QF=QB�����BP��QP��⣻
��3������������εı߳����ٸ�������ȵ������Ʊ߳��ȵ�ƽ�������S��AGN=![]() ��������S�ı���GHMN=S��AHM-S��AGN��⣮
��������S�ı���GHMN=S��AHM-S��AGN��⣮
���������(1)��E��F�ֱ���������ABCD��BC��CD���е㣬
��CF=BE��
��Rt��ABE��Rt��BCF ���BAE=��CBF
���ߡ�BAE+��BEA=900�����CBF+��BEA=900��
���BGE=900�� ��AE��BF
(2)��������ã�FP=FC����PFB=��BFC����FPB=900��
��CD��AB, ���CFB=��ABF��
���ABF=��PFB����QF=QB
��PF=k��k>O������PB=2k��
��Rt��BPQ����QB=x�� ��x2=(x��k)2+4k2, ��x=![]() k��
k��
��sin��BQP=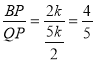
(3) �ı���GHMN�������![]() .
.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�