题目内容
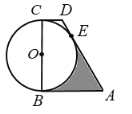
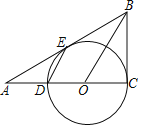
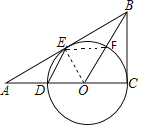
【题目】如图,点D、O在△ABC的边AC上,以CD为直径的⊙O与边AB相切于点E,连结DE、OB,且DE∥OB.
(1)求证:BC是⊙O的切线.
(2)设OB与⊙O交于点F,连结EF,若AD=OD,DE=4,求弦EF的长.
【答案】(1)见解析;(2)4
【解析】
(1)连接OE,根据切线的性质得到OE⊥AB,根据平行线的性质得到∠BOC=∠EDO,∠BOE=∠DEO,根据全等三角形的性质得到∠OCB=∠OEB=90°,于是得到BC是⊙O的切线;
(2)根据直角三角形的性质得到OD=DE=4,推出四边形DOFE是平行四边形,得到EF=OD=4.
(1)证明:连接OE,
∵以CD为直径的⊙O与边AB相切于点E,
∴OE⊥AB,
∵DE∥OB,
∴∠BOC=∠EDO,∠BOE=∠DEO,
∵OE=OD,
∴∠EDO=∠DEO,
∴∠BOC=∠BOE,
∵OB=OB,OC=OE,
∴△OCB≌△OEB(SAS),
∴∠OCB=∠OEB=90°,
∴BC是⊙O的切线;
(2)解:∵∠AEO=90°,AD=OD,
∴ED=![]() AO=OD,
AO=OD,
∴OD=DE=4,
∵DE∥OF,DE=OD=OF,
∴四边形DOFE是平行四边形,
∴EF=OD=4,
∴弦EF的长为4.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目