Question

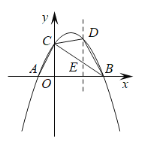
【题目】如图，在平面直角坐标系中，已知抛物线与x轴交于A（-1，0），B（3，0）两点，与y轴交于点C．

(1)求该抛物线的解析式；

(2)如图①，若点D是抛物线上一动点，设点D的横坐标为m（0＜m＜3），连接CD，BD，BC，AC，当△BCD的面积等于△AOC面积的2倍时，求m的值；

(3)若点N为抛物线对称轴上一点，请在图②中探究抛物线上是否存在点M，使得以B，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点M的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）（2）1或2（3）存在；M1（2，2）M2（-2，）M3（4，）

【解析】

（1）将A、B两点坐标代入抛物线解析式求出a、b即可得到解析式；

（2）过点D作y轴平行线交BC于点E，用m表示出D、E的坐标，求出DE线段的表达式，再利用面积关系建立方程求解；

（3）根据平行四边形对角线互相平分，可知对角线上的两个点的中点相同，可用中点坐标公式建立方程求解，设N(1,n)，M(x,y)，分3种情况讨论即可.

（1）把A（-1，0），B（3，0）代入中，得：

解得：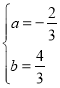

∴抛物线解析式为

（2）过点D作y轴平行线交BC于点E

把代入中，得：，

∴C点坐标是（0，2），又B（3,0）

∴直线BC的解析式为

∵

∴

∴

由得：

∴

整理得：

解得 ，

∵0＜m＜3

∴m的值为1或2

（3）存在点M使得以B，C，M，N为顶点的四边形是平行四边形，

设N(1,n)，M(x,y)，

四边形CMNB是平行四边形时，CN、MB为对角线，

∴

∴x=2，代入抛物线得

∴M（-2，）；

四边形CNBM时平行四边形时，CB、MN为对角线，

∴，

∴x=2，代入抛物线得

∴M(2,2)；

四边形CNMB时平行四边形时，CM、BN为对角线，

∴，

∴x=4，代入抛物线得

∴M（4，）；

综上所述：存在M1（2，2）M2（-2，）M3（4，）