Question

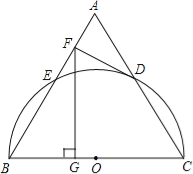
【题目】如图，AD是∠BAC的平分线，DE平行AB交AC于点E，DF平行AC交AB于点F，延长FE交BC的延长线于点G．

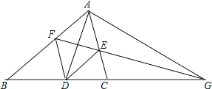
求证：

（1）AG＝DG；

（2）∠GAC＝∠B．

Answer 1

【答案】（1）详见解析；（2）详见解析

【解析】

（1）由DE∥AB，DF∥AC，可证得四边形AEDF是平行四边形，∠DAF＝∠ADE，又由AD是∠BAC的平分线，可证得AE＝DE，即可证得四边形AEDF是菱形，则可得EF是AD的垂直平分线，继而证得结论；

（2）由AG＝DG，AE＝DE，可得∠GAD＝∠GDA，∠EAD＝∠EDA，继而证得∠GAC＝∠GDE，又由DE∥AB，可得∠GDC＝∠B，继而证得结论．

证明：（1）∵DE∥AB，DF∥AC，

∴四边形AEDF是平行四边形，∠DAF＝∠ADE，

∵AD是∠BAC的平分线，

∴∠DAF＝∠DAE，

∴∠DAE＝∠ADE，

∴AE＝DE，

∴四边形AEDF是菱形，

∴EF是AD的垂直平分线，

∵延长FE交BC的延长线于点G，

∴AG＝DG；

（2）∵AG＝DG，AE＝DE，

∴∠GAD＝∠GDA，∠EAD＝∠EDA，

∵∠GAC＝∠GAD﹣∠EAD，∠GDE＝∠GDA﹣∠EDA，

∴∠GAC＝∠GDE，

∵DE∥AB，

∴∠GDE＝∠B，

∴∠GAC＝∠B．