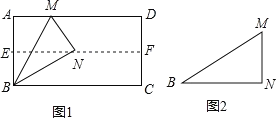
��Ŀ����
����Ŀ��ijˮ�����������ڣ������Ϊ10Ԫ/���ij��ˮ�����������ν��ۺ�ļ۸�Ϊ8.1Ԫ/��������ν��۵İٷ�����ͬ��
��1�������ˮ��ÿ�ν��۵İٷ��ʣ�
��2���ӵ�һ�ν��۵ĵ�1�����𣬵�x�죨xΪ���������ۼۡ��������������ķ��õ������Ϣ�����ʾ����֪����ˮ���Ľ���Ϊ4.1Ԫ/������۸�ˮ����x���죩������Ϊy��Ԫ������y��x��1��x��14��֮��ĺ�����ϵʽ��������ڼ���ʱ�����������

���𰸡���1��10%����2��![]() ����10���������
����10���������
��������
��1��������ٷ�����x������ij��Ʒԭ��Ϊ10Ԫ�����ڸ���ԭ���������ν��ۣ����ۺ�ļ۸�Ϊ8.1Ԫ�����з�����⣻
��2����������ȡֵ�ȼ��㣬��1��x��7ʱ����8��x��14ʱ��������=���ۼ�-���ۣ���������-�����к�����ϵʽ�������������������ֵ�����Աȣ�
�⣺��1�������ˮ��ÿ�ν��۵İٷ�����x��
10��1��x��2��8.1��
x��10%��x��190%����ȥ����
�𣺸���ˮ��ÿ�ν��۵İٷ�����10%��
��2����1��x��7ʱ����1�ν��ۺ�ļ۸�10����1��10%����9��
��y����9��4.1����80��3x������40+3x��
����17.7x+352��
�ߩ�17.7��0��
��y��x�����������
�൱x��1ʱ��y�����ֵ��y������17.7��1+352��334.3��Ԫ����
��8��x��14ʱ����2�ν��ۺ�ļ۸�8.1Ԫ��
��y����8.1��4.1����120��x������3x2��64x+400��
����3x2+60x+80
����3��x��10��2+380��
�൱x��10ʱ��y�����ֵ��y����380��Ԫ����
����������y��x��1��x��15��֮��ĺ�����ϵʽΪ��
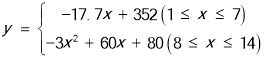
��10����������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ�������ۼ�x��Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3���������Ҫ���ÿ�첻����1350Ԫ�������ҷ��ϳ����Լ��Ĺ涨����ô����Ʒÿǧ���ۼ۵�ȡֵ��Χ�Ƕ��٣���˵�����ɣ�
����Ŀ��ij�̵깺��һ���ɱ�Ϊÿ��40Ԫ����Ʒ�����̵갴���۲����ڳɱ��ۣ��Ҳ�����70Ԫ���ۣ������۵���Ϊ�������������鷢�֣�����Ʒÿ���������y(��)�����۵���x(Ԫ)֮��Ĺ�ϵ�����
���۵���x/Ԫ | 40 | 50 | 60 | 70 |
ÿ���������y/�� | 140 | 120 | 100 | 80 |
(1)������������������������ݣ�����ѧ����һ�κ����������������Ͷ��κ����е�һ������ʾy��x֮��ı仯���ɣ�˵��ѡ�����ֺ��������ɣ���������ĺ�������ʽ���Ա�����ȡֵ��Ȧ��
(2)���۵��۶�Ϊ����Ԫʱ������ʹ���۸���Ʒÿ���õ����������������Ƕ���Ԫ��