题目内容
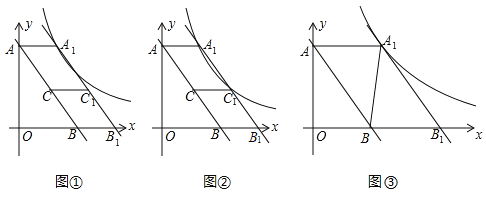
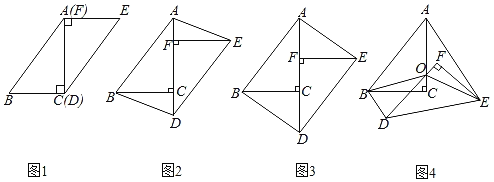
【题目】在一次数学研究性学习中，小兵将两个全等的直角三角形纸片ABC和DEF拼在一起，使点A与点F重合，点C与点D重合（如图1），其中∠ACB＝∠DFE＝90°，BC＝EF＝3cm，AC＝DF＝4cm，并进行如下研究活动．
活动一：将图1中的纸片DEF沿AC方向平移，连结AE，BD（如图2），当点F与点C重合时停止平移．
（思考）图2中的四边形ABDE是平行四边形吗？请说明理由．
（发现）当纸片DEF平移到某一位置时，小兵发现四边形ABDE为矩形（如图3）．求AF的长．
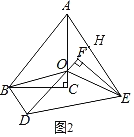
活动二：在图3中，取AD的中点O，再将纸片DEF绕点O顺时针方向旋转α度（0≤α≤90），连结OB，OE（如图4）．
（探究）当EF平分∠AEO时，探究OF与BD的数量关系，并说明理由．
【答案】【思考】是，理由见解析；【发现】
；【探究】BD＝2OF，理由见解析；
【解析】
【思考】由全等三角形的性质得出AB＝DE，∠BAC＝∠EDF，则AB∥DE，可得出结论；
【发现】连接BE交AD于点O，设AF＝x（cm），则OA＝OE＝
（x+4），得出OF＝OA﹣AF＝2﹣x，由勾股定理可得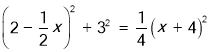
，解方程求出x，则AF可求出；
【探究】如图2，延长OF交AE于点H，证明△EFO≌△EFH（ASA），得出EO＝EH，FO＝FH，则∠EHO＝∠EOH＝∠OBD＝∠ODB，可证得△EOH≌△OBD（AAS），得出BD＝OH，则结论得证．
解：【思考】四边形ABDE是平行四边形．
证明：如图，∵△ABC≌△DEF，
∴AB＝DE，∠BAC＝∠EDF，
∴AB∥DE，
∴四边形ABDE是平行四边形；
【发现】
如图1，连接BE交AD于点O，
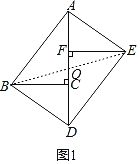
∵四边形ABDE为矩形，
∴OA＝OD＝OB＝OE，
设AF＝x（cm），则OA＝OE＝（x+4），
∴OF＝OA﹣AF＝2﹣x，
在Rt△OFE中，∵OF2+EF2＝OE2，
∴，
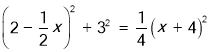解得：x＝，
∴AF＝cm．
【探究】BD＝2OF，
证明：如图2，延长OF交AE于点H，
∵四边形ABDE为矩形，
∴∠OAB＝∠OBA＝∠ODE＝∠OED，OA＝OB＝OE＝OD，
∴∠OBD＝∠ODB，∠OAE＝∠OEA，
∴∠ABD+∠BDE+∠DEA+∠EAB＝360°，
∴∠ABD+∠BAE＝180°，
∴AE∥BD，
∴∠OHE＝∠ODB，
∵EF平分∠OEH，
∴∠OEF＝∠HEF，
∵∠EFO＝∠EFH＝90°，EF＝EF，
∴△EFO≌△EFH（ASA），
∴EO＝EH，FO＝FH，
∴∠EHO＝∠EOH＝∠OBD＝∠ODB，
∴△EOH≌△OBD（AAS），
∴BD＝OH＝2OF．
