题目内容
【题目】“切实减轻学生课业负担”是我市作业改革的一项重要举措．某中学为了解本校学生平均每天的课外作业时间，随机抽取部分学生进行问卷调查，并将调查结果分为A、B、C、D四个等级，A：1小时以内；B：1小时--1.5小时；C：1.5小时--2小时；D：2小时以上．根据调查结果绘制了如图所示的两种不完整的统计图，请根据图中信息解答下列问题：
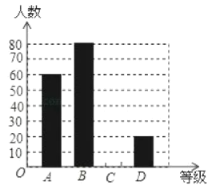
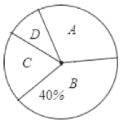
（1）该校共调查了多少名学生？
（2）请将条形统计图补充完整；
（3）在此次调查问卷中，甲、乙两班各有2人平均每天课外作业量都是2小时以上，从这4人中人选2人去参加座谈，用列表或画树状图的方法求选出的2人来自不同班级的概率．
【答案】（1）该校共调查了200名学生；（2）详见解析；（3）
【解析】
（1）根据B类的人数和所占的百分比即可求出总数．
（2）求出C的人数从而补全统计图．
（3）先设甲班学生为为
，乙班学生为
，根据题意画出树形图，再根据概率公式列式计算即可．
解：（1）共调查的中学生人数是：
（人），
答：该校共调查了200名学生；
（2）C类的人数是：
（人），补图如下：
（3）设甲班学生为，乙班学生为，树状图如下：
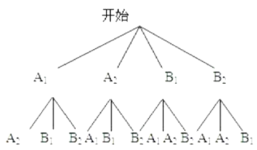
一共有12种等可能结果，其中2人来自不同班级共有8种，
∴P（2人来自不同班级）
．
【题目】某商店购进一批成本为每件40元的商品，若商店按单价不低于成本价，且不高于70元销售，且销售单价为正整数，经调查发现，该商品每天的销售量y(件)与销售单价x(元)之间的关系如表：
销售单价x/元 | 40 | 50 | 60 | 70 |
每天的销售量y/件 | 140 | 120 | 100 | 80 |
(1)请你认真分析表中所给的数据，用你学过的一次函数、反比例函数和二次函数中的一种来表示y与x之间的变化规律，说明选择这种函数的理由，并求出它的函数表达式和自变量的取值范圈．
(2)销售单价定为多少元时，才能使销售该商品每天获得的利润最大？最大利润是多少元？
