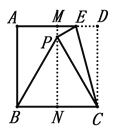题目内容
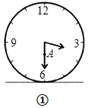
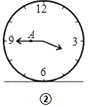
【题目】如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:
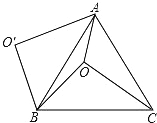
①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;
②连接OO′,则OO′=4;
③∠AOB=150°;
④S四边形AOBO′=6+4![]() .
.
其中正确的结论是 .
【答案】①②③④
【解析】
试题解析:如图,连接OO′;
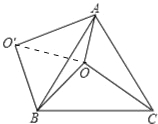
∵△ABC为等边三角形,
∴∠ABC=60°,AB=CB;
由题意得:∠OBO′=60°,OB=O′B,
∴△OBO′为等边三角形,∠ABO′=∠CBO,
∴OO′=OB=4;∠BOO′=60°,
∴选项②正确;
在△ABO′与△CBO中,
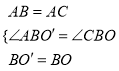 ,
,
∴△ABO′≌△CBO(SAS),
∴AO′=OC=5,
△BO′A可以由△BOC绕点B逆时针方向旋转60°得到,
∴选项①正确;
在△AOO′中,∵32+42=52,
∴△AOO′为直角三角形,
∴∠AOO′=90°,∠AOB=90°+60°=150°,
∴选项③正确;
∵S四边形AOBO′=![]() ,
,
∴选项④正确.
综上所述,正确选项为①②③④.

 阅读快车系列答案
阅读快车系列答案【题目】如图,在平行四边形ABCD的边AD的延长线上截取DE=AD,F是AE延长线上的一点,连结BD、CE、BF分别交CE、CD于G、H.
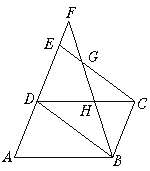
求证:(1)△ABD≌△DCE;
(2)CE∶CG=DF∶AD.
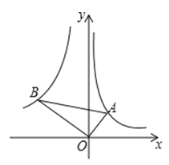
【题目】问题:探究函数y=x+![]() 的图象和性质.
的图象和性质.
小华根据学习函数的方法和经验,进行了如下探究,下面是小华的探究过程,请补充完整:
(1)函数的自变量x的取值范围是:____;
(2)如表是y与x的几组对应值,请将表格补充完整:
x | … | ﹣3 | ﹣2 | ﹣ | ﹣1 |
|
| 1 |
| 2 | 3 | … |
y | … | ﹣3 | ﹣3 |
| ﹣3 | ﹣4 | 4 |
| 3 | … |
(3)如图,在平面直角坐标系中描点并画出此函数的图象;
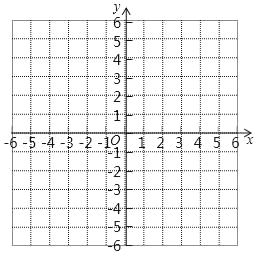
(4)进一步探究:结合函数的图象,写出此函数的性质(一条即可).