题目内容
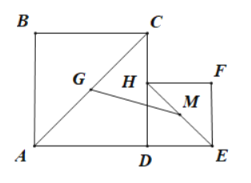
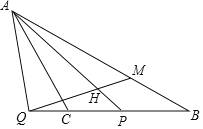
【题目】如图,已知等腰△ABC,∠ACB=120°,P是线段CB上一动点(与点C,B不重合),连接AP,延长BC至点Q,使得∠PAC=∠QAC,过点Q作射线QH交线段AP于H,交AB于点M,使得∠AHQ=60°.
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示);
(2)用等式表示线段QC和BM之间的数量关系,并证明.
【答案】(1)∠AMQ=30°+α;(2)BM![]() CQ,证明见解析.
CQ,证明见解析.
【解析】
(1)根据等腰△ABC,∠ACB=120,得到∠B=∠CAB=30°,由∠ACQ=60°.
∠AHQ=60°,可得∠AGH=∠QGC,则有∠MQB=∠PAC=α,利用三角形的外角的性质,可知∠AMQ=30°+α;
(2)过点M作ME∥AC,交BQ于点E,根据∠PAC=∠QAC=α,∠QAM=∠QMA=30°+α,可得QA=QM,∠ACQ=∠MEQ=60,利用AAS可证△QAC≌△MQE,可以得出EM=EB,设EN=x,则BE=EM=2x,BN![]() x,可得BM=2
x,可得BM=2![]() x,CQ=EM=2x,可求出 BM
x,CQ=EM=2x,可求出 BM![]() CQ.
CQ.
(1)如图
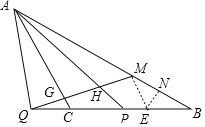
∠ACB=120°,AC=BC,
∴∠B=∠CAB=30°,∠ACQ=60°.
∵∠AHQ=60°.
∵∠AGH=∠QGC,∴∠MQB=∠PAC=α
∠AMQ=∠B+∠MQB=30°+α;
(2)如图,

过点M作ME∥AC,交BQ于点E,
∵∠PAC=∠QAC=α,
∴∠QAM=∠QMA=30°+α,
∴QA=QM
∴∠ACQ=∠MEQ=60°,∠QAC=∠MQE,
∴△QAC≌△MQE(AAS),∴CQ=EM
∵∠B=30°,∴∠EMB=30°,∴EM=EB,
作EN⊥BM于点N,
设EN=x,则BE=EM=2x,BN![]() x,∴BM=2
x,∴BM=2![]() x,
x,
CQ=EM=2x,∴BM![]() CQ.
CQ.

 阶梯计算系列答案
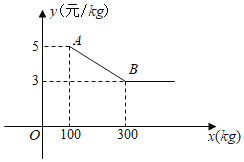
阶梯计算系列答案【题目】如图1,长度为6千米的国道![]() 两侧有
两侧有![]() ,
,![]() 两个城镇,从城镇到公路分别有乡镇公路连接,连接点为
两个城镇,从城镇到公路分别有乡镇公路连接,连接点为![]() 和
和![]() ,其中
,其中![]() 、
、![]() 之间的距离为2千米,
之间的距离为2千米,![]() 、
、![]() 之间的距离为1千米,
之间的距离为1千米,![]() 、
、![]() 之间的乡镇公路长度为2.3千米,
之间的乡镇公路长度为2.3千米,![]() 、
、![]() 之间的乡镇公路长度为3.2千米,为了发展乡镇经济,方便两个城镇的物资输送,现需要在国道
之间的乡镇公路长度为3.2千米,为了发展乡镇经济,方便两个城镇的物资输送,现需要在国道![]() 上修建一个物流基地
上修建一个物流基地![]() ,设
,设![]() 、
、![]() 之间的距离为
之间的距离为![]() 千米,物流基地
千米,物流基地![]() 沿公路到
沿公路到![]() 、
、![]() 两个城镇的距离之和为
两个城镇的距离之和为![]() 干米,以下是对函数
干米,以下是对函数![]() 随自变量
随自变量![]() 的变化规律进行的探究,请补充完整.
的变化规律进行的探究,请补充完整.
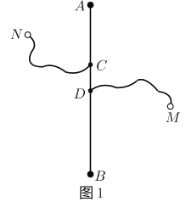
(1)通过取点、画图、测量,得到![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 10.5 | 8.5 | 6.5 | 10.5 | 12.5 |
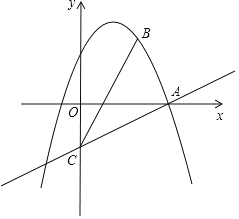
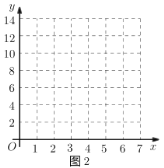
(2)如图2,建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:
①若要使物流基地![]() 沿公路到
沿公路到![]() 、
、![]() 两个城镇的距离之和最小,则物流基地
两个城镇的距离之和最小,则物流基地![]() 应该修建在何处?(写出所有满足条件的位置)
应该修建在何处?(写出所有满足条件的位置)
答:__________.
②如右图,有四个城镇![]() 、
、![]() 、
、![]() 、
、![]() 分别位于国道
分别位于国道![]() 两侧,从城镇到公路分别有乡镇公路连接,若要在国道上修建一个物流基地
两侧,从城镇到公路分别有乡镇公路连接,若要在国道上修建一个物流基地![]() ,使得
,使得![]() 沿公路到
沿公路到![]() 、
、![]() 、
、![]() 、
、![]() 的距离之和最小,则物流基地
的距离之和最小,则物流基地![]() 应该修建在何处?(写出所有满足条件的位置)
应该修建在何处?(写出所有满足条件的位置)
答:__________.