题目内容
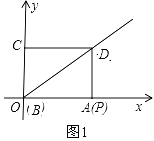
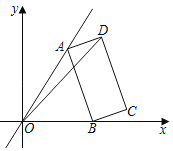
【题目】如图,在平面直角坐标系中,点A在一次函数y=![]() x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2
x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2![]() ,AD=1,则OD的最大值是( )
,AD=1,则OD的最大值是( )
A.![]() B.
B.![]() +2C.
+2C.![]() +2D.
+2D.![]()
【答案】B
【解析】
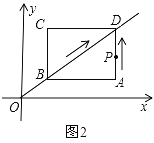
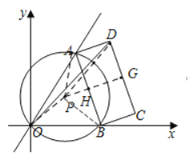
作△AOB的外接圆⊙P,连接OP、PA、PB、PD,作PG⊥CD,交AB于H,垂足为G,易得∠APH=∠AOB,解直角三角形求得PH=2,然后根据三角形三边关系得出OD取最大值时,OD=OP+PD,据此即可求得.
解:∵点A在一次函数y=![]() x图象上,∴tan∠AOB=
x图象上,∴tan∠AOB=![]() ,
,
作△AOB的外接圆⊙P,连接OP、PA、PB、PD,作PG⊥CD,交AB于H,垂足为G,
∵四边形ABCD是矩形,
∴AB∥CD,四边形AHGD是矩形,
∴PG⊥AB,GH=AD=1,
∵∠APB=2∠AOB,∠APH=![]() ∠APB,AH=
∠APB,AH=![]() AB=
AB=![]() =DG,
=DG,
∴∠APH=∠AOB,
∴tan∠APH=tan∠AOB=![]() ,
,
∴![]() =
=![]() ,
,
∴PH=1,
∴PG=PH+HG=1+1=2,
∴PD=![]() =
=![]() =
=![]() ,
,
∴OP=PA=![]() =
=![]() =2,
=2,
在△OPD中,OP+PD≥OD,
∴OD的最大值为:OP+PD=2+![]() ,
,
故选:B.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
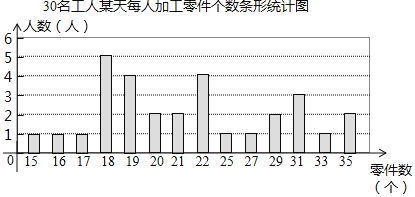
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
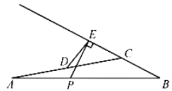
【题目】如图,在![]() 中,
中,![]() ,点D是
,点D是![]() 边的中点,点P是边
边的中点,点P是边![]() 上的一个动点,过点P作射线
上的一个动点,过点P作射线![]() 的垂线,垂足为点E,连接
的垂线,垂足为点E,连接![]() .设
.设![]() ,
,![]() .小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
.小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如表:
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.4 |
y/cm | 1.6 | 1.3 | 1.0 | 0.9 | 1.0 | 1.3 | 2.1 | 2.5 | 2.9 |
(说明:补全表格时相关数据保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:点E是![]() 边的中点时,
边的中点时,![]() 的长度约为________cm.
的长度约为________cm.