题目内容
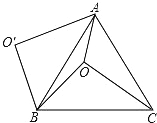
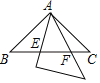
【题目】在Rt△ACB中,∠ACB=90°,点D为AB上一点.
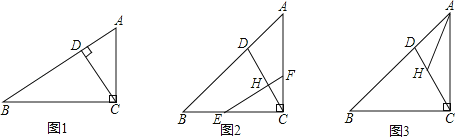
(1)如图1,若CD⊥AB,求证:CD2=ADDB;
(2)如图2,若AC=BC,EF⊥CD于H,EF与BC交于E,与AC交于F,且![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)如图3,若AC=BC,点H在CD上,且∠AHD=45°,CH=3DH,直接写出tan∠ACH的值为 .
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证出∠B=∠ACD,证明△CBD∽△ACD,得出CD:AD=BD:CD,即可得出结论;
(2)设FH=4a,则HE=9a(a>0),同(1)得CH2=HEFH=36a2,则CH=6a,在Rt△CHF中,tan∠ACD=![]() =
=![]() ,过D作DP⊥AC于P,则DP∥BC,在Rt△DPC中,tan∠ACD=
,过D作DP⊥AC于P,则DP∥BC,在Rt△DPC中,tan∠ACD=![]() =
=![]() ,△ADP是等腰直角三角形,得出AP=DP,求出
,△ADP是等腰直角三角形,得出AP=DP,求出![]() =
=![]() =
=![]() ,由平行线分线段成比例定理即可得出答案;
,由平行线分线段成比例定理即可得出答案;
(3)过点D作DM⊥AH于M,设DH=2x,则CH=6x(x>0),CD=DH+CH=8x,证明△ADH∽△CDA,得出∠DAH=∠ACH,AD:CD=DH:AD,求出AD=4x,证明△ADM是等腰直角三角形,得出DM=HM=![]() DH=
DH=![]() x,由勾股定理得出AM=
x,由勾股定理得出AM=![]() x,由三角函数定义即可得出答案.
x,由三角函数定义即可得出答案.
(1)证明:∵CD⊥AB,
∴∠ADC=∠CDB=90°,
∵∠ACB=90°,
∴∠B+∠BCD=∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴△CBD∽△ACD,
∴CD:AD=BD:CD,
∴CD2=ADDB;
(2)∵![]() =
=![]() ,
,
∴设FH=4a,则HE=9a(a>0),
∵∠ACB=90°,EF⊥CD,
∴同(1)得:CH2=HEFH=9a×4a=36a2,
∴CH=6a,
在Rt△CHF中,tan∠ACD=![]() =
=![]() =
=![]() ,
,
过D作DP⊥AC于P,如图2所示:
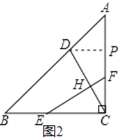
则DP∥BC,
在Rt△DPC中,tan∠ACD=![]() =
=![]() ,
,
∵AC=BC,∠ACB=90°,
∴∠A=45°,
∴△ADP是等腰直角三角形,
∴AP=DP,
∴![]() =
=![]() =
=![]() ,
,
∵DP∥BC,
∴![]() =
=![]() =
=![]() ;
;
(3)过点D作DM⊥AH于M,如图3所示:
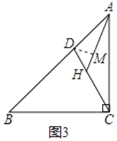
∵CH=3DH,
∴设DH=2x,则CH=6x(x>0),
∴CD=DH+CH=8x,
∵AC=BC,∠ACB=90°,
∴∠BAC=45°=∠AHD,
又∵∠ADH=∠CDA,
∴△ADH∽△CDA,
∴∠DAH=∠ACH,AD:CD=DH:AD,
∴AD2=DHCD=16x2,
∴AD=4x,
∵DM⊥AH,∠AHD=45°,
∴△ADM是等腰直角三角形,
∴DM=HM=![]() DH=
DH=![]() x,
x,
∴AM=![]() =
=![]() =
=![]() x,
x,
∴tan∠ACH=tan∠DAH=![]() =
=![]() =
=![]() ;
;
故答案为:![]() .
.