题目内容
【题目】如图,在平行四边形ABCD的边AD的延长线上截取DE=AD,F是AE延长线上的一点,连结BD、CE、BF分别交CE、CD于G、H.
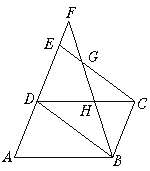
求证:(1)△ABD≌△DCE;
(2)CE∶CG=DF∶AD.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据平行四边形的性质得到DC=AB,∠EDC=∠DAB,再根据DE=AD,即可证明△ABD≌△DCE;
(2)先证明四边形DBCE是平行四边形,根据平行的性质得到∠CGB=∠DBF
证明:(1) ∵四边形DBCE为平行四边形,
∴DC=AB,∠EDC=∠DAB,
又∵DE=AD,
在△ABD和△DCE中,
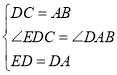
所以△ABD≌△DCE(SAS);
(2)∵四边形ABCD是平行四边形,F是AE延长线上的一点,
∵DE=AD,DE∥BC,
∴DE=AD=BC(等量替换),
∴四边形DBCE是平行四边形,
∴EC∥DB,∠GCB=∠BDF,
∴∠CGB=∠DBF,
∴△DBF∽△CGB,
由△DBF∽△CGB,可得![]() ,
,
又∵CE=DB,CB=AD,
∴![]() ,
,
即CE∶CG=DF∶AD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目