题目内容
【题目】如图,平面直角坐标系中,已知A(2,2)、B(4,0),若在x轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
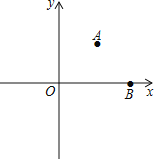
A. 1B. 2C. 3D. 4
【答案】D
【解析】
由点A、B的坐标可得到AB=2![]() ,然后分类讨论:若AC=AB;若BC=AB;若CA=CB,确定C点的个数.
,然后分类讨论:若AC=AB;若BC=AB;若CA=CB,确定C点的个数.
∵点A、B的坐标分别为(2,2)、B(4,0).
∴AB=2![]() ,
,
如图,①若AC=AB,以A为圆心,AB为半径画弧与x轴有2个交点(含B点),即(0,0)、(4,0),
∴满足△ABC是等腰三角形的C点有1个;
②若BC=AB,以B为圆心,BA为半径画弧与x轴有2个交点,即满足△ABC是等腰三角形的C点有2个;
③若CA=CB,作AB的垂直平分线与x轴有1个交点,即满足△ABC是等腰三角形的C点有1个;
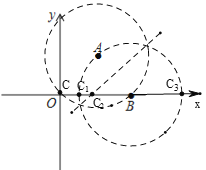
综上所述:点C在x轴上,△ABC是等腰三角形,符合条件的点C共有4个.
故选D.

练习册系列答案
相关题目