题目内容
【题目】教材母题 点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0).设△OPA的面积为S.
(1)用含有x的式子表示S,写出x的取值范围,画出函数S的图象;
(2)当点P的横坐标为5时,△OPA的面积为多少?
(3)△OPA的面积能大于24吗?为什么?
【答案】(1) S=-3x+24, 0<x<8.(2) 9.(3)能.
【解析】(1)根据三角形的面积公式列式,即可用含x的解析式表示S,然后根据S>0及已知条件,可求出x的取值范围,根据一次函数的性质可画出函数S的图象;
(2)将x=5代入(1)中所求解析式,即可求出△OPA的面积;
(3)根据一次函数的性质及自变量的取值范围即可判断.
解:(1)∵点A和点P的坐标分别是(6,0),(x,y),
∴S=![]() ×6×y=3y.
×6×y=3y.
∵x+y=8,
∴y=8-x.
∴S=3(8-x)=24-3x.
∴S=-3x+24.
∵点P在第一象限,
∴x>0,y>0,
即x>0,8-x>0.
∴0<x<8.
图象如图所示.
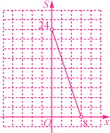
(2)当x=5时,S=-3×5+24=9.
(3)能.理由:令S>24,
则-3x+24>24.
解得x<0.
∵由(2)得0<x<8,
∴△OPA的面积不能大于24.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目

