题目内容
【题目】如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA﹣AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是![]() cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
(1)用含x的代数式表示线段AP的长.
(2)当点P在线段BA上运动时,求y与x之间的函数关系式.
(3)当经过点B′和△ADC一个顶点的直线平分△ADC的面积时,直接写出x的值.

【答案】(1)当![]() 时,PA=5t,当1<x<5时,
时,PA=5t,当1<x<5时,![]()
(2)y=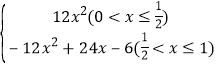 ;(3)x=
;(3)x=![]() s或
s或![]() s或
s或![]() s时,经过点B′和△ADC一个顶点的直线平分△ADC的面积.
s时,经过点B′和△ADC一个顶点的直线平分△ADC的面积.
【解析】分析:(1)分两种情形讨论即可.
(2)分两种情形①如图1中,当![]() 时,重叠部分是四边形PBQB′.
时,重叠部分是四边形PBQB′.
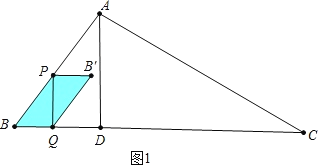
②如图2中,当![]() 重叠部分是五边形PBQMN.分别求解即可.
重叠部分是五边形PBQMN.分别求解即可.
(3)分三种情形①如图3中,当PA=B时,PB′是△ABD是中位线.②如图4中,设AB′的延长线交BC于G.③如图5中,连接DB′交AC于N,延长B′P交AD于T,作NM⊥PB′于M,NH⊥AD于H.分别构建方程即可解决问题.
详解:(1)当![]() 时,PA=5t,
时,PA=5t,
当1<x<5时,![]()
(2)如图1中,当![]() 时,重叠部分是四边形PBQB′.
时,重叠部分是四边形PBQB′.
∵PQ⊥BC,AD⊥BC,
∴PQ∥AD,
∴![]()
∴![]()
∴PQ=4x,BQ=3x,
由题意四边形PBQB′是平行四边形,
∴![]()
如图2中,当![]() 重叠部分是五边形PBQMN.
重叠部分是五边形PBQMN.
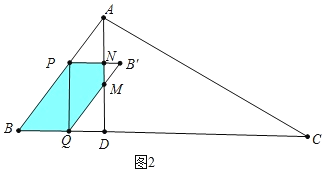
∵PN∥BD,
∴![]()
∴PN=3(1x),B′N=3x3(1x)=6x3,易知MN=4(2x
∴![]()
综上所述,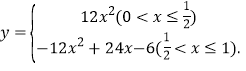
(3)如图3中,当PA=B时,PB′是△ABD是中位线。
∴AB′=DB′,此时CB′平分△ADC的面积,此时![]() .
.
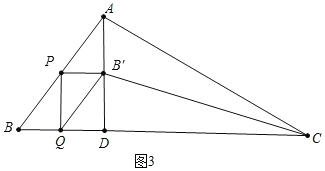
如图4中,设AB′的延长线交BC于G.
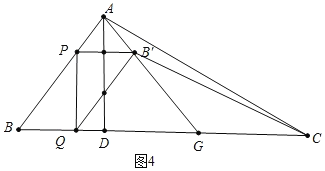
当DG=GC=4时,AB′平分△ADC的面积,
∵PB′∥BG,
∴![]() ∴
∴![]()
∴![]()
如图5中,连接DB′交AC于N,延长B′P交AD于T,作NM⊥PB′于M,NH⊥AD于H.
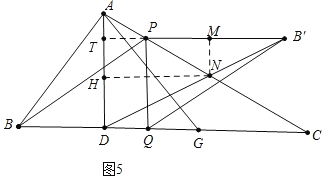
由题意PA=![]() (x1),AT=x1,TP=2(x1),PB′=BQ=3+2(x1)=2x+1,
(x1),AT=x1,TP=2(x1),PB′=BQ=3+2(x1)=2x+1,
当AN=CN时,DB′平分△ADC的面积,
∴可得AH=HD=2,HN=TM=2,
∴B′M=TB′MT=2(x1)+2x+14=4x5,MN=2(x1)=3x,TD=4(x1)=5x,
∵MN∥TD,
∴![]()
∴![]()
∴![]()
综上所述,x=![]() s或
s或![]() s或
s或![]() s时,经过点B′和△ADC一个顶点的直线平分△ADC的面积。
s时,经过点B′和△ADC一个顶点的直线平分△ADC的面积。