Question

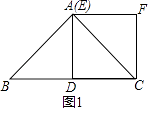
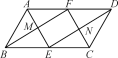
【题目】如图，ABCD中，∠ABC＝60°，AB＝4，AD＝8，点E，F分别是边BC，AD的中点，点M是AE与BF的交点，点N是CF与DE的交点，则四边形ENFM的周长是______．

Answer 1

【答案】4＋4

【解析】

连接EF，点E、F分别是边BC、AD边的中点，可知BE=AF=AB=4，可证四边形ABEF为菱形，根据菱形的性质可知AE⊥BF，且AE与BF互相平分，∠ABC=60°，△ABE为等边三角形，ME=F=4，由勾股定理求MF，根据菱形的性质可证四边形MENF为矩形，再求四边形ENFM的周长．

解：连接EF，

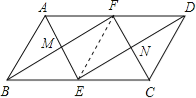
∵点E、F分别是边BC、AD边的中点，

∴BE=AF=AB=4，

又AF∥BE，

∴四边形ABEF为菱形，由菱形的性质，得AE⊥BF，且AE与BF互相平分，

∵∠ABC=60°，∴△ABE为等边三角形，ME=F=4，

在Rt△MEF中，由勾股定理，得MF=，

由菱形的性质，可知四边形MENF为矩形，

∴四边形ENFM的周长=2（ME+MF）=4+4．

故答案为：4+4