题目内容
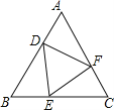
【题目】如图,在等边三角形ABC的三边上,分别取点D、E、F,使AD=BE=CF,
(1)求证:△DEF是等边三角形.
(2)若2BE=EC,求∠FEC的度数.
【答案】(1)见解析;(2)∠FEC=30°
【解析】
(1)由△ABC是等边三角形,AD=BE=CF,易证得△ADF≌△BED,即可得DF=DE,同理可得DF=EF,即可证得:△DEF是等边三角形.
(2)取EC的中点H,连接FH.只要证明FH=CH=EH,可得∠EFC=90°.
(1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,
∵AD=BE=CF,
∴AF=BD,
在△ADF和△BED中,
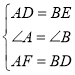 ,
,
∴△ADF≌△BED(SAS),
∴DF=DE,
同理DE=EF,
∴DE=DF=EF.
∴△DEF是等边三角形.
(2)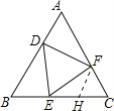
解:取EC的中点H,连接FH.
∵EC=2BE,EH=CH,BE=CF,
∴CH=CF,
∵∠C=60°,
∴△CFH都是等边三角形,
∴FH=CH=EH,
∴∠EFC=90°
∴∠FEC=30°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目