题目内容
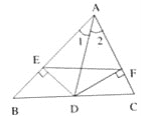
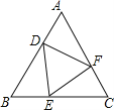
【题目】如图,在△ABC中,∠ACB=105°,AC边上的垂直平分线交AB边于点D,交AC边于点E,连结CD.
(1)若AB=10,BC=6,求△BCD的周长;
(2)若AD=BC,试求∠A的度数.
【答案】(1)16;(2)25°.
【解析】
根据线段垂直平分线的性质,可得CD=AD,根据三角形的周长公式,可得答案;根据线段垂直平分线的性质,可得CD=AD,根据等腰三角形的性质,可得∠B与∠CDB的关系,根据三角形外角的性质,可得∠CDB与∠A的关系,根据三角形内角和定理,可得答案.
解:(1)∵DE是AC的垂直平分线,
∴AD=CD.
∵C△BCD=BC+BD+CD=BC+BD+AD=BC+AB,
又∵AB=10,BC=6,
∴C△BCD=16;
(2)∵AD=CD
∴∠A=∠ACD,
设∠A=x,
∵AD=CB,
∴CD=CB,
∴∠CDB=∠CBD.
∵∠CDB是△ACD的外角,
∴∠CDB=∠A+∠ACD=2x,
∵∠A、∠B、∠ACB是三角形的内角,
∵∠A+∠B+∠ACB=180°,
∴x+2x+105°=180°,
解得x=25°
∴∠A=25°.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(1)分别求A、B两种型号的净水器的销售单价;
(2)若该电器公司准备用不多于54000元的金额采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?