Question

【题目】已知，如图，在平行四边形ABCD中，BF平分∠ABC交AD于点F，AE⊥BF于点O，交BC于点E，连接EF．

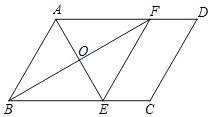
（1）求证：四边形ABEF是菱形；

（2）若AE＝12，BF＝16，CE＝5，求四边形ABCD的面积．

Answer 1

【答案】（1）见解析；（2）四边形ABCD的面积为144．

【解析】

（1）根据平行四边形对边平行的性质和BF平分∠ABC，可得∠AFB＝∠ABF，进而得出AB=AF，再证明△ABO≌△EBO得AB=BE，最后得出四边形ABEF是菱形；
（2）作AG⊥BC于点G，根据勾股定理以及菱形的性质先求出BE的长，再利用菱形面积公式求出AG的长，最后即可求得四边形ABCD的面积．

（1）证明：∵四边形ABCD是平行四边形，

∴AD∥BC，∴∠AFB＝∠FBE，

∵BF平分∠ABC，∴∠ABF＝∠EBF，

∴∠AFB＝∠ABF，∴AF＝AB，

∵AE⊥BF，∴∠AOB＝∠EOB＝90°，

又OB＝OB，∠ABO＝∠EBO，

∴△ABO≌△EBO（ASA），

∴AB＝BE=AF，

又AF∥BE，

∴四边形ABEF是平行四边形，

∵AB＝BE，

∴平行四边形ABEF是菱形；

（2）如图，作AG⊥BC于点G，

∵四边形ABEF是菱形，

∴OE＝AE＝6，OB＝BF＝8，

∴在Rt△OBE中，BE＝＝10．

又S菱形ABEF=×AE×BF=BE×AG，

∴×12×16=10×AG，∴AG＝．

∴四边形ABCD的面积为：BCAG＝（10+5）×＝144．