题目内容
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
【答案】解:(1)∵A、B两点关于对称轴![]() 对称 ,且A点的坐标为(-3,0),
对称 ,且A点的坐标为(-3,0),
∴点B的坐标为(1,0)。
(2)①∵抛物线![]() ,对称轴为
,对称轴为![]() ,经过点A(-3,0),
,经过点A(-3,0),
∴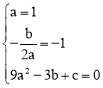 ,解得
,解得![]() 。
。
∴抛物线的解析式为![]() 。
。
∴B点的坐标为(0,-3)。∴OB=1,OC=3。∴![]() 。
。
设点P的坐标为![]() ,则
,则![]() 。
。
∵![]() ,∴
,∴![]() ,解得
,解得![]() 。
。
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴点P的坐标为(2,5)或(-2,-3)。
②设直线AC的解析式为![]() ,将点A,C的坐标代入,得:
,将点A,C的坐标代入,得:
![]() ,解得:
,解得:![]() 。
。
∴直线AC的解析式为![]() 。
。
∵点Q在线段AC上,∴设点Q的坐标为![]() 。
。
又∵QD⊥x轴交抛物线于点D,∴点D的坐标为![]() 。
。
∴![]() 。
。
∵![]() ,∴线段QD长度的最大值为
,∴线段QD长度的最大值为![]() 。
。
【解析】(1)由抛物线的对称性直接得点B的坐标。
(2)①用待定系数法求出抛物线的解析式,从而可得点C的坐标,得到![]() ,设出点P 的坐标,根据
,设出点P 的坐标,根据![]() 列式求解即可求得点P的坐标。
列式求解即可求得点P的坐标。
②用待定系数法求出直线AC的解析式,由点Q在线段AC上,可设点Q的坐标为![]() ,从而由QD⊥x轴交抛物线于点D,得点D的坐标为
,从而由QD⊥x轴交抛物线于点D,得点D的坐标为![]() ,从而线段QD等于两点纵坐标之差,列出函数关系式应用二次函数最值原理求解。
,从而线段QD等于两点纵坐标之差,列出函数关系式应用二次函数最值原理求解。

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目