题目内容
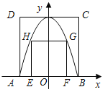
【题目】已知二次函数![]() 的图象如图所示,有以下结论:
的图象如图所示,有以下结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]()
其中所有正确结论的序号是( )

A. ①②④ B. ①③④ C. ②③⑤ D. ①②④⑤
【答案】D
【解析】
利用抛物线开口方向得到a<0,利用抛物线的对称轴b=2a<0,可对②进行判断;
利用抛物线与y轴的交点坐标得到c>0,则可对①进行判断;
根据抛物线与x轴有2个交点可对③进行判断;
根据抛物线的对称性得到抛物线与x轴的另一个交点在((-3,0)与(-2,0)之间,则x=-2时,y>0,于是可对④进行判断;
利用c=1,a<0可对⑤进行判断.
:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-![]() =-1,
=-1,
∴b=2a<0,即2a-b=0,所以②正确;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc>0,所以①正确;
∵抛物线与x轴有2个交点,
∴b2-4ac>0,所以③错误;
∵抛物线与x轴的另一个交点在(-3,0)与(-2,0)之间,
∴x=-2时,y>0,即4a-2b+c>0,所以④正确;
∵c=1,a<0,
∴c-a=1-a>1,所以⑤正确.
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】由于雾霾天气持续笼罩某地区,口罩市场出现热卖.某商店用8000元购进甲、乙两种口罩,销售完后共获利2800元,其进价和售价如下表:
甲种口罩 | 乙种口罩 | |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该商店购进甲、乙两种口罩各多少袋?
(2)该商店第二次仍以原价购进甲、乙两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍,甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,则乙种口罩最低售价为每袋多少元?