Question

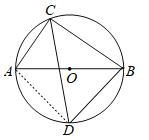
【题目】如图，AB是⊙O的直径，AC是⊙O的弦，∠ACB的平分线交⊙O于点D.若AC=6，BC=8，则BD＝__________.

Answer 1

【答案】

【解析】

根据直径得出∠ACB=∠ADB=90°，根据勾股定理求出AB的长度．根据直径所对的圆周角是直角可得∠ACB=∠ADB=90°，再根据角平分线的定义可得∠DAC=∠BCD，然后求出AD=BD，再根据等腰直角三角形的性质求解即可．

连接AD．

∵AB是直径，∴∠ACB=∠ADB=90°（直径所对的圆周角是直角）．在Rt△ABC中，AC=6，BC=8，∴AB===10．

∵AB是直径，∴∠ACB=∠ADB=90°．

∵∠ACB的平分线交⊙O于点D，∴∠DCA=∠BCD，∴=，∴AD=BD，∴在Rt△ABD中，AD=BD=AB=×10=5，即BD=5．

故答案为：5．