Question

【题目】已知：如图∠BAC的角平分线与BC的垂直平分线交于点D，DE⊥AB，DF⊥AC，垂足分别为点E，F．

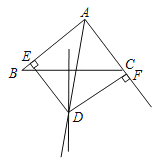
（1）求证：BE＝CF；

（2）如果AB＝10，AC＝8，求BE的长．

Answer 1

【答案】（1）见解析；（2）BE＝1.

【解析】

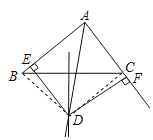
（1）连接BD、CD，由垂直平分线的性质得出BD=CD，由角平分线的性质得出DE=DF，由HL证得Rt△BDE≌Rt△CDF，即可得出结论；
（2）由HL证得Rt△ADE≌Rt△ADF，得出AE=AF，则AB-BE=AC+CF，推出BE+CF=AB-AC=2，由BE=CF，即可得出结果．

（1）证明：连接BD、CD，如图所示：

∵BC的垂直平分线过点D，

∴BD＝CD，

∵点D是∠BAC的角平分线上的点，DE⊥AB，DF⊥AC，

∴DE＝DF，

在Rt△BDE和Rt△CDF中， ，

∴Rt△BDE≌Rt△CDF（HL），

∴BE＝CF；

（2）解：在Rt△ADE和Rt△ADF中， ，

∴Rt△ADE≌Rt△ADF（HL），

∴AE＝AF，

∴AB﹣BE＝AC+CF，

∴BE+CF＝AB﹣AC＝10﹣8＝2，

∵BE＝CF，

∴．