Question

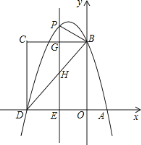
【题目】如图，在平面直角坐标系中，抛物线与轴交于、两点，与轴交于点，四边形是矩形，点的坐标为，点的坐标为，已知点是线段上的动点，过点作轴交抛物线于点，交于点，交于点．

求该抛物线的解析式；

当点在直线上方时，请用含的代数式表示的长度；

在的条件下，是否存在这样的点，使得以、、为顶点的三角形与相似？若存在，求出此时的值；若不存在，请说明理由．

Answer 1

【答案】 ；，

【解析】

（1）将D（-4，0），B（0，4）代入，运用待定系数法即可求出抛物线的解析式；
（2）先求出抛物线与直线BC的交点，再求PG的长度.
（3）根据相似三角形对应边成比例列出比例关系式，进而求出m的值．

∵四边形是正方形，点坐标为，

∴点的坐标是，

∵点和点在抛物线上

∴，

∴，

∴该抛物线的解析式为：；

∵，解得或，

∴抛物线与直线的交点为，

∴点在直线上方时，的取值范围是：，

∵，，

∵轴交抛物线于点，交于点，

∴，，

∴，

∵抛物线的解析式为：；

设点，

∴，，

∵，

∴，

∵，

∴，，

∵以、、为顶点的三角形与相似且，

∴，

∴，

∴，

∴，

∴或（舍）

即：.