题目内容
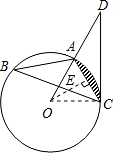
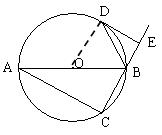
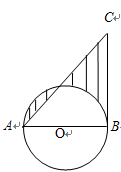
如图,已知:△ABC是⊙O的内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°.

(1)判断直线CD与⊙O的位置关系,并说明理由.
(2)若AC=6,求图中弓形(即阴影部分)的面积.

(1)判断直线CD与⊙O的位置关系,并说明理由.
(2)若AC=6,求图中弓形(即阴影部分)的面积.
(1)直线CD是⊙O的切线,理由见解析(2)6π-9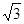
(1)直线CD是⊙O的切线
理由如下:
如图,连接OC
∵∠AOC、∠ABC分别是AC所对的圆心角、圆周角
∴∠AOC=2∠ABC=2×30°=60°………………………………2分
∴∠D+∠AOC=30°+60°=90°
∴∠DCO=90°………………………………3分
∴CD是⊙O的切线………………………………4分
(2)过O作OE⊥AC,点E为垂足
∵OA=OC,∠AOC=60°
∴△AOC是等边三角形
∴OA=OC=AC=6,∠OAC=60°………………………………6分
在Rt△AOE中:OE=OA•sin∠OAC=6•sin60°=3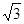
∴S△AOC=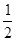 ×6×3
×6×3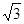 =9
=9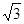
∵S扇形AOC=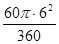 =6π
=6π
∴S阴=S扇形AOC-S△AOC=6π-9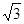 ………………………………8分
………………………………8分
(1)连接OC.欲证明DE是⊙O的切线,只需证明DE⊥OC即可;
(2)利用弓形的面积等于扇形的面积减去三角形的面积计算阴影部分的面积即可.
理由如下:
如图,连接OC
∵∠AOC、∠ABC分别是AC所对的圆心角、圆周角
∴∠AOC=2∠ABC=2×30°=60°………………………………2分
∴∠D+∠AOC=30°+60°=90°
∴∠DCO=90°………………………………3分
∴CD是⊙O的切线………………………………4分
(2)过O作OE⊥AC,点E为垂足
∵OA=OC,∠AOC=60°
∴△AOC是等边三角形
∴OA=OC=AC=6,∠OAC=60°………………………………6分
在Rt△AOE中:OE=OA•sin∠OAC=6•sin60°=3
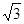
∴S△AOC=
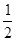 ×6×3
×6×3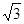 =9
=9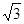
∵S扇形AOC=
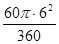 =6π
=6π∴S阴=S扇形AOC-S△AOC=6π-9
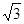 ………………………………8分
………………………………8分
(1)连接OC.欲证明DE是⊙O的切线,只需证明DE⊥OC即可;
(2)利用弓形的面积等于扇形的面积减去三角形的面积计算阴影部分的面积即可.

练习册系列答案
相关题目
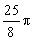
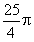
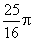
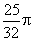

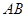 是⊙
是⊙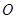 的直径,
的直径,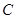 、
、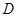 在圆上,已知∠
在圆上,已知∠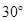 ,
,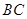 =
=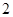 ,则
,则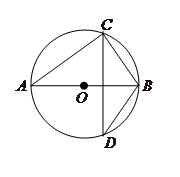
 上异于E、H的点.若∠A=50°,则∠EPH= .
上异于E、H的点.若∠A=50°,则∠EPH= .