题目内容
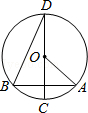
已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于D,DE
与⊙O相切,交CB的延长线于E.
⑴ 判断直线AC和DE是否平行,并说明理由;
⑵ 若∠A=30°,BE=1cm,分别求线段DE和 的长。(直接写出最后结果).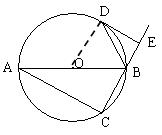
与⊙O相切,交CB的延长线于E.
⑴ 判断直线AC和DE是否平行,并说明理由;
⑵ 若∠A=30°,BE=1cm,分别求线段DE和 的长。(直接写出最后结果).

.⑴ 平行 ;
理由是:
联结OD,∵DE与⊙O相切,
∴ OD⊥DE.
∵ OB=OD, ∴∠ODB=∠OBD.
∵ BD是∠ABE的平分线,
即∠ABD=∠DBE,
∴ ∠ODB=∠DBE.
∴ OD∥BE.
∴ BE⊥DE,即DE⊥CE.
∵ AB是⊙O的直径,点C在⊙O上,∴AC⊥CE
∴ AC∥DE.
⑵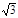 ,
,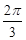 .
.
理由是:
联结OD,∵DE与⊙O相切,
∴ OD⊥DE.
∵ OB=OD, ∴∠ODB=∠OBD.
∵ BD是∠ABE的平分线,
即∠ABD=∠DBE,
∴ ∠ODB=∠DBE.
∴ OD∥BE.
∴ BE⊥DE,即DE⊥CE.
∵ AB是⊙O的直径,点C在⊙O上,∴AC⊥CE
∴ AC∥DE.
⑵
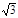 ,
,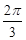 .
. (1)平行.连接OD,∵DE与⊙O相切,得出OD⊥DE.根据BD是∠ABE的平分线,推出∠ODB=∠DBE,得到OD∥BE.推出BE⊥DE,根据AB是⊙O的直径,得到AC⊥CE,即可推出答案;
(2)由∠A=30°,根据三角形的外角性质求出∠DBE,即可求出DE,根据弧长公式即可求出弧BD的长.
(2)由∠A=30°,根据三角形的外角性质求出∠DBE,即可求出DE,根据弧长公式即可求出弧BD的长.

练习册系列答案
相关题目

 轴相切于坐标原点O(0,0),与
轴相切于坐标原点O(0,0),与 轴相交于点A(5,0),过点A的直线AB与
轴相交于点A(5,0),过点A的直线AB与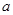 , D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同
, D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同 ,函数
,函数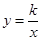 的图象经过点
的图象经过点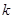 的值(用含
的值(用含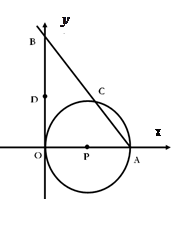
 半径为3cm,
半径为3cm,